Properties of a Parallelogram
A quadrilateral has four sides, four angles and four vertices. A

Activity: Make a random parallelogram from a sheet of paper. Draw one of its diagonals and cut along it. We now have two triangles. What can be said about both these triangles?
Try placing one triangle over the other. As it turns out, both the two triangles are congruent to each other. Try doing it a few more times with different parallelograms.
Now, let's prove this result.
Theorem: A diagonal of a parallelogram divides it into two congruent triangles.
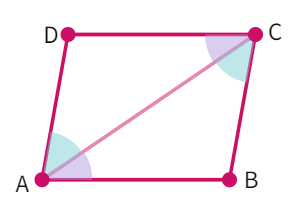
Proof: Let ABCD be a parallelogram and AC be a diagonal. The diagonal AC divides parallelogram ABCD into two triangles, namely, ∆ ABC and ∆ CDA.
- From the figure, we know: BC || AD and AC is a
. - We see: ∠ BCA = ∠
(Pair of alternate angles). - Similarly, AB || DC and AC is a transversal.
- ∠ BAC = ∠
(Pair of alternate angles) - AC =
as they are a common side. - ∆ ABC ≅ ∆
by congruency rule. - Diagonal AC divides parallelogram ABCD into two congruent triangles ABC and CDA
Theorem : If a quadrilateral is a parallelogram, then each pair of its opposite sides is equal.

- We already know that ∆ ABC ≅ ∆
by congruency rule. - Since, the corresponding parts of congruent triangles are also equal: AB =
and = BC - Thus, opposite sides of a parallelogram are equal.
Theorem : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
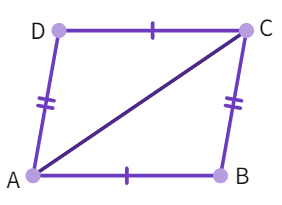
- Taking a quadrilateral where AB =
and AD = - With the diagonal AC drawn, we get ∆ABC and ∆CDA where:
- AD = BC and CD = AB are given
- AC =
as it is a side - Thus, ∆ ABC ≅ ∆
by congruency rule. - From CPCT, we get: ∠ BAC = ∠
and ∠ BCA = ∠ - These are alternate interior angles for the quadrilateral ABCD.
- Since, alternate interior angles are equal- quadrilateral ABCD is a parallelogram.
Therefore, in a parallelogram each pair of opposite sides is equal and conversely if each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Theorem : In a parallelogram, opposite angles are equal

- We know that when the diagonal of a parallelogram is drawn, we get two congruent triangles.
- With the diagonal AC drawn, we get ∆ ABC ≅ ∆
- Thus from CPCT, we get: ∠ ABC = ∠
which (as seen) are opposite angles. - Similarly, if we draw diagonal BD, we get ∆ BCD ≅ ∆
- From CPCT, we get: ∠BCD = ∠
- These are opposite angles of a parallelogram.
- Thus, the opposite angles of a parallelogram are equal.
Now, is the converse true?
Theorem : If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
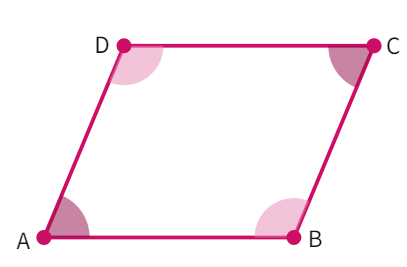
- We have quadrilateral ABCD with ∠ABC = ∠ADC and ∠DAB = ∠BCD.
- We also know: ∠ABC + ∠ADC + ∠DAB + ∠BCD =
° (angle sum property) - Combining the angle sum with the fact that opposite angles are equal we get: ∠ABC + ∠
= ° - In a pair of parallel lines being cut through with a transverse, the co-interior angles are
. - Thus, we can say: AD ∥
with as transverse - Similarly, we get ∠ABC + ∠
= ° - Which again, gives us: AB ∥
with as transverse. - Since, both the opposite sides are
, quadrilateral ABCD is a .
Theorem : The diagonals of a parallelogram bisect each other.
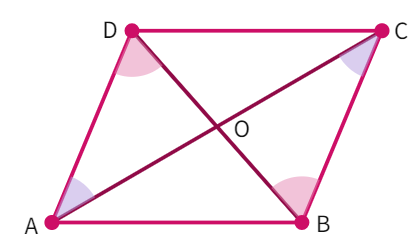
- We have parallelogram ABCD with AB || DC and AD||BC.
- Considering triangles ∆ AOD and ∆ COB, we get: AD =
as sides are equal - ∠ DAO = ∠
and ∠ ADO = ∠ ( interior angles are equal) - By
congruency, ∆ AOD ≅ ∆ - By CPCT, AO =
and BO = - Thus, diagonals of a parallelogram bisect each other.
Theorem: If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
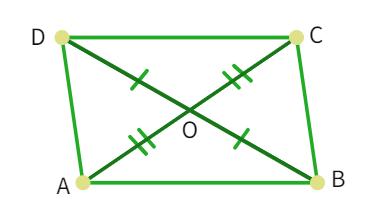
- We have been given: OA = OC and OB = OD
- Considering the triangles ∆ AOB and ∆ COD: ∠ AOB = ∠
(vertically angles) - OA =
and = OD - ∆
≅ ∆ COD by congruency rule. - Therefore, ∠ OAB = ∠
- These are alternate interior angles to the lines AB and CD and are
. - Thus, AB ||
- A similar argument can made for ∆ AOD and ∆ COB, which gives us: BC ||
- Since, quadrilateral ABCD has parallel opposite sides, ABCD is a
.
Example 1 : Show that each angle of a rectangle is a right angle.
Solution : Let us recall what a rectangle is. A rectangle is a parallelogram in which one angle is a right angle. Let ABCD be a rectangle in which ∠ A = 90°. We have to show that ∠ B = ∠ C = ∠ D = 90° We have, AD || BC and AB is a transversal (see Fig. 8.6). So, ∠ A + ∠ B = 180° (Interior angles on the same side of the transversal) But, ∠ A = 90° So, ∠ B = 180° – ∠ A = 180° – 90° = 90° Now, ∠ C = ∠ A and ∠ D = ∠ B (Opposite angles of the parallellogram) So, ∠ C = 90° and ∠ D = 90°. Therefore, each of the angles of a rectangle is a right angle.
Example 2: Prove that the diagonals of a rhombus are perpendicular to each other.
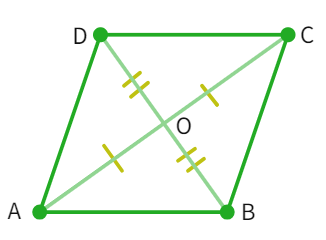
- Rhombus is a
having . - Thus, from the figure: AB =
= CD = - Considering, the triangles ∆ AOD and ∆ COD, we get: OA = OC ( as
) - OD =
as it is a side - AD =
(given) - By
congruency rule: ∆ AOD ≅ ∆ - By CPCT, we get: ∠ AOD = ∠
- We also know that: ∠ AOD + ∠ COD =
° - Thus, we get:
∠ AOD = 180° which further gives us: ∠ AOD = ° - Thus, the diagonals of a rhombus are perpendicular to each other.
Example 3: ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || AB. Show that:
(i) ∠ DAC = ∠ BCA
(ii) ABCD is a parallelogram
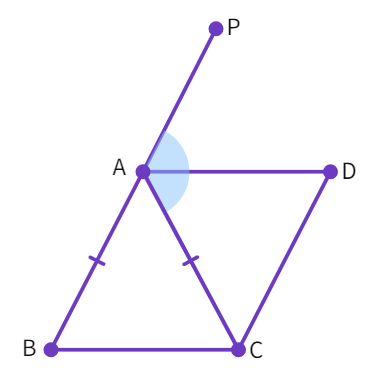
- Given: ∆ ABC is isosceles in which AB = AC
- Thus, ∠ ABC = ∠
(Angles to equal sides) - Using exterior angle property: ∠ PAC = ∠ ABC + ∠
- Which gives us: ∠ PAC =
∠ ACB (i) - Also given: AD bisects ∠ PAC i.e. ∠ PAC = 2 ∠
(ii) - Combining (i) and (ii) we get: ∠ DAC = ∠
- Further on, equal angles ∠ DAC and ∠ ACB form a pair of alternate angles where line segments BC and AD are intersected by a transversal line
. - Thus, BC ||
- Also given: BA ||
- Since the opposite sides of the quadrilateral ABCD are parallel, ABCD is a parallelogram.
Example 4: Two parallel lines l and m are intersected by a transversal p. Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
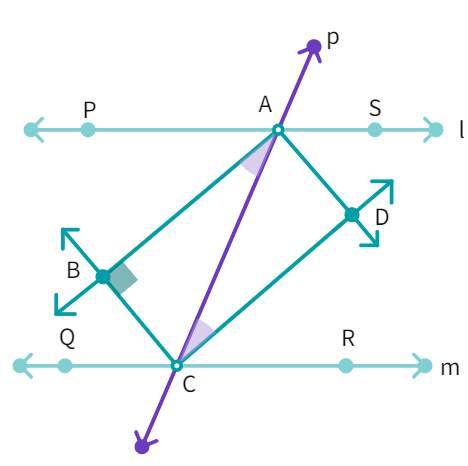
- Given: PS || QR and transversal p intersects them at points A and C respectively.
- Also given: The bisectors of ∠ PAC and ∠ ACQ intersect at B and bisectors of ∠ ACR and ∠ SAC intersect at D.
- From the figure: ∠ PAC = ∠ ACR (Alternate angles as l || m and p is a transversal)
- Thus,
1 2 ∠ ACR which gives us ∠ = ∠ - Equal angles ∠ BAC and ∠ ACD form a pair of alternate angles for the lines AB and DC with
as transversal. - So, AB ||
- Similarly, we can conclude that angles ∠ ACB = ∠
- Thus, BC ||
- Therefore, quadrilateral ABCD is a
- From the figure: ∠ PAC + ∠ CAS =
° - Dividing the whole equation by
1 2 + ∠ = ° - This gives us ∠ BAD =
° - Since, ABCD is a parallelogram with one angle equal to 90°, it is a rectangle.
Example 5 : Show that the bisectors of angles of a parallelogram form a rectangle. Solution : Let P, Q, R and S be the points of intersection of the bisectors of ∠ A and ∠ B, ∠ B and ∠ C, ∠ C and ∠ D, and ∠ D and ∠ A respectively of parallelogram ABCD (see Fig. 8.10). In ∆ ASD, what do you observe? Since DS bisects ∠ D and AS bisects ∠ A, therefore,
∠ DAS + ∠ ADS =
Therefore, PQRS is a parallelogram in which one angle (in fact all angles) is 90° and so, PQRS is a rectangle.
