The Mid-point Theorem
Let's now, move on to some important results related to the mid-point of the sides of a triangle.
Activity: On a piece of paper, draw a triangle ABC and mark the mid-points E and F of two sides (AB and AC in this case) of the triangle. Join the points E and F.
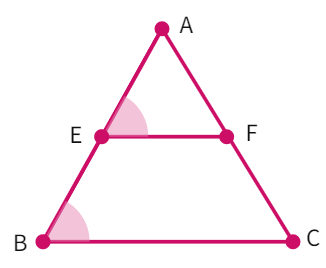
Using a ruler and protractor, measure:
EF and BC
∠ AEF and ∠ ABC
What observation can be made? We see that :
EF =
Since, ∠ AEF is equal to ∠ ABC with AB acting as a transverse, we can say that:
EF || BC
Theorem : The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
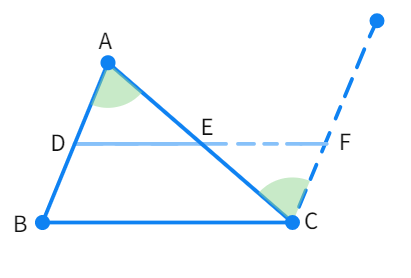
We have D and E as the mid-points of the sides AB and AC. Join both the points and extend DE further. Also draw a line parallel to the side AB from point C. Let the point at which the extended DE line and the line parallel to AB intersect be point F.
- Considering the triangles △ADE and △CFE: AE =
( is the midpoint) - ∠DAE = ∠
( they are interior angles) and ∠AED = ∠ ( vertically angles) - Thus, by
congruency rule: △ADE ≅ △ - By CPCT: AD =
and DE = - Thus, we see BD = AD = CF. Since, we have BD = CF and BD ∥ CF (by construction) : BCFD is a
- This further tells us: ED ∥
(Opposite sides of a parallelogram) - This also means: EF ∥
- Thus, the line segment joining the mid points of a triangle is parallel to the third side.
- Hence, proved.
But, what about the length of this line segment ? Let's find out.
- We have already proved that: DE =
- We also have that: DE +
= DF = BC (Opposite sides of the parallelogram) - We can write:
EF = BC - Thus,
= BC - Thus, we have found the length of the segment.
Therefore,
The line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half as long as the third side.
Now, is the converse true? Let's find out.
Theorem : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
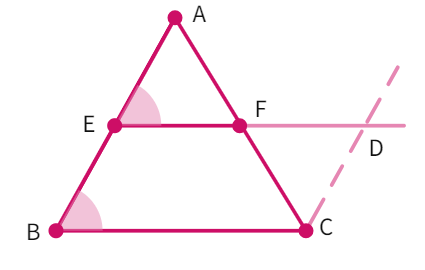
Here, we have been given that:
EF ∥ BC
Now, let's extend this side EF upto a certain point. Also draw a line parallel to the side AB from point C. Let the point of intersection of these constructed lines be point D.
Now, we have a parallelogram BCDE, since the opposite sides are all parallel.
- We have: BE =
( sides of parallelogram) - BE =
(Midpoint of side ).Thus, AE = - Considering the triangles △AEF and △CDF, we have: AE = CD (Proved), ∠AEF = ∠
( interior angles) - And ∠AFE = ∠
(vertically opposite angle) - By
congruency criterion: △AEF ≅ △ - By CPCT: AF =
i.e. F is the of AC - Hence, proved.
Example 6: In ∆ ABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ∆ ABC is divided into four congruent triangles by joining D, E and F.
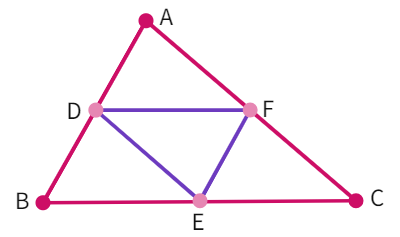
- D and E are
of sides AB and BC of the triangle ABC. - Thus, DE||
(Line segment joining midpoints is parallel to third side) - Similarly we get: DF ||
and EF || - Therefore, ADEF, BDFE and DFCE are all
. - We know that: a diagonal of a parallelogram divides it into two
triangles. is a diagonal of the parallelogram BDFE. - Therefore, ∆ BDE ≅ ∆
- Similarly, ∆
≅ ∆ FED and ∆ ≅ ∆ FED. - Thus, all the four triangles are congruent.
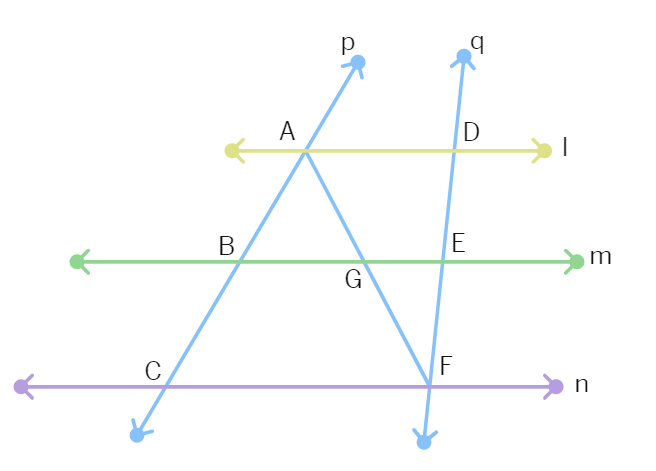
Example 7 : l, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p. Show that l, m and n cut off equal intercepts DE and EF on q also.
Solution: