Moderate Level Worksheet
Very Short Answer Questions (1 Mark Each)
(1) Write the condition under which a line is a tangent to a circle.
A line is tangent to a circle when:
Perfect! A tangent touches the circle at exactly one point and is perpendicular to the radius at that point.
(2) If the distance from the external point to the center is 10 cm and the radius is 6 cm, what is the length of the tangent?
Using Pythagorean theorem:
Length =
Excellent! The tangent length is 8 cm.
(3) Name the geometric figure formed by joining two radii.
Two radii form a
Correct! Two radii and the arc between them form a sector.
(4) In a circle, what is the maximum number of tangents that can be drawn from an exterior point?
Maximum number of tangents from an external point:
Perfect! Exactly two tangents can be drawn from any external point.
(5) What kind of triangle is formed by joining the center of a circle and the ends of a tangent?
The triangle formed is:
Excellent! The tangent is perpendicular to the radius, forming a right triangle.
(6) What is the measure of angle formed by two tangents drawn from an external point to a circle when the angle at the center is 60°?
If angle at center = 60°, then angle between tangents =
Perfect! The angles are supplementary: tangent angle + center angle = 180°.
(7) Can two circles have a common tangent? Justify with a reason.
Reason:
Correct! Two circles can have up to 4 common tangents depending on their relative positions.
(8) State whether the following is true or false: "A tangent can intersect a circle at two points."
A tangent touches the circle at
Perfect! If a line intersects a circle at two points, it's called a secant, not a tangent.
Short Answer Questions (2 Marks Each)
Note: Answer each question with steps and explanation, in 2-3 sentences. Write down the answers on sheet and submit to the school subject teacher.
(1) The radius of a circle is 7 cm. A point lies 25 cm away from the center. Find the length of the tangent drawn from the point.
Excellent! The tangent length is 24 cm using the tangent-radius relationship: Tangent length =
(2) From an external point, two tangents are drawn to a circle and the angle between the tangents is 60°. Find the angle subtended by the line joining the center to the external point at the center. Angle at center = θ =
Perfect! The angle at the center is 120° since, Angle between tangents + Angle at center = 180°
(3) Prove that the tangents drawn from an external point to a circle are equally inclined to the line joining the point and the center.
(4) Draw a circle of radius 3 cm and construct two tangents to it from a point 6 cm away from the center. Measure and write the length of the tangents.
Perfect! The measured length should match the calculated value.
(5) Two tangents TP and TQ are drawn to a circle with center O from an external point T. Prove that ∠OTP = ∠OTQ.

Excellent! This proves the tangents are equally inclined to the line of centers.
(6) Find the length of the tangent if the distance between the center and the external point is 17 cm and the radius is 8 cm.
Tangent length =
Perfect! The tangent length is 15 cm.
(7) In the figure, PT and QT are tangents drawn from point T to a circle with center O. If ∠PTQ = 70°, find ∠POQ.
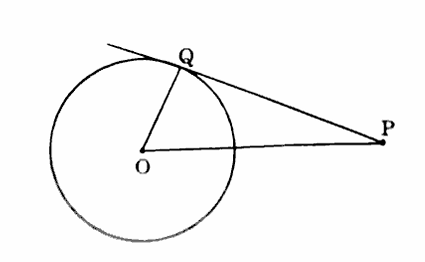
∠POQ =
Excellent! The reflex angle ∠POQ = 110°.
(8) A triangle is formed by joining the center of the circle and points of contact of two tangents. What is the nature of the triangle? Justify.
The triangle formed is
Justification: The two sides from center to points of contact are
Perfect! The triangle is isosceles because two sides are radii (equal length).
Long Answer Questions (4 Marks Each)
Note: Answer each question with steps and explanation. Write down the answers on sheet and submit to the school subject teacher.
(1) Construct a circle of radius 4 cm. Mark a point 8 cm away from the center. Construct two tangents from the external point and measure their length. Also verify the result using the Pythagoras theorem.
Tangent length =
Excellent! The measured and calculated values should match.
(2) A tangent is drawn to a circle from an external point A. The center of the circle is O and the radius is 6 cm. If OA = 10 cm, find the length of the tangent and prove that the triangle formed is a right triangle.
Tangent length:
Perfect! Tangent length = 8 cm, and the triangle is right-angled at T.
(3) Two tangents are drawn from an external point P to a circle with center O. Prove that the triangle formed by the center and the two points of contact is isosceles.
(4) In a circle, two chords AB and AC are such that ∠ABC = 90°. Prove that the line joining the midpoints of AB and AC is equal in length to the tangent drawn from B to the circle.
(5) A tangent and a secant are drawn from an external point P to a circle with center O. Prove that the square of the length of the tangent is equal to the product of the lengths of the secant segment and its external part.
Part B: Objective Questions (1 Mark Each)
Choose the correct answer and write the option (a/b/c/d)
(1) The triangle formed by the center of a circle and the ends of a tangent is:
(a) Right triangle (b) Scalene triangle (c) Equilateral (d) Obtuse triangle
Correct! The tangent is perpendicular to the radius, forming a right triangle.
(2) If a tangent from an external point is 12 cm long and the radius of the circle is 5 cm, the distance from the center to the point is:
(a) 13 cm (b) 7 cm (c) 10 cm (d) 17 cm
Correct! Using Pythagoras:
(3) The number of tangents that can be drawn to two externally touching circles is:
(a) 2 (b) 3 (c) 4 (d) Infinite
Correct! Two externally touching circles have 3 common tangents: 2 external and 1 internal (at the point of contact).
(4) The length of the tangent from a point P to a circle is 8 cm. If the distance between P and the center is 10 cm, what is the radius of the circle?
(a) 6 cm (b) 5 cm (c) √36 cm (d) 4 cm
Correct!
(5) If the tangents from a point P to a circle with center O are drawn, then triangle △POT is always:
(a) Isosceles (b) Equilateral (c) Scalene (d) Right-Angled
Correct! The triangle is always right-angled at T because the tangent is perpendicular to the radius.
(6) The angle between two tangents drawn from an external point is:
(a) 90° (b) 180° (c) Depends on the position of the point (d) Always 60°
Correct! The angle varies depending on how far the external point is from the circle.
(7) The length of a tangent from an external point to a circle is shortest when:
(a) The point is on the circle (b) The point is at infinity (c) The point lies on the line joining the center and the point of contact (d) None of the above
Correct! When the point is on the circle, the tangent length is 0 (shortest possible).
(8) If the radius of a circle is r and the distance from the external point to the center is d, then the length of the tangent is:
(a)
Correct! This is derived from the Pythagorean theorem in the right triangle formed.
(9) If ∠OTP = 45°, where T is a point on the circle and P is an external point, then angle between the two tangents is:
(a) 90° (b) 60° (c) 45° (d) 135°
Correct! Since ∠OTP = 45° and tangents are equally inclined, the angle between tangents = 2 × 45° = 90°.
(10) The perpendicular from the center of the circle to a chord ? the chord.
(a) Divides (b) Bisects (c) Is tangent to (d) Has no relation with
Correct! The perpendicular from the center to a chord always bisects the chord.
Tangents and Secants Challenge
Determine whether these statements about tangents and secants are True or False:
