Exercise 4.3

1. Which of the following pairs of angles are supplementary?

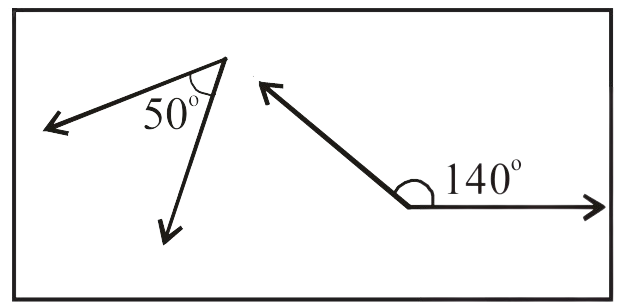
(i)

110° + 70° = °

These are a pair of angles as their sum is 110° + 70° = 180°.

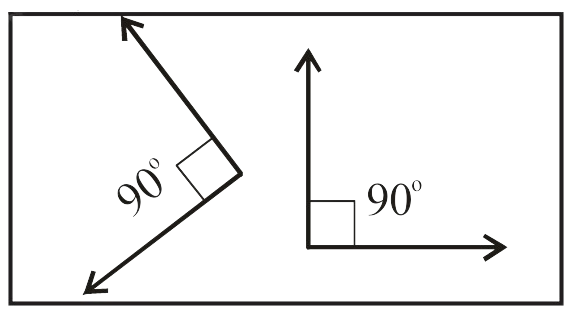
(ii)

There are a pair of angles as their sum is 90° + 90° = °.

(iii)

These are pair of supplementary angles because their sum is 50° + 140° = °.

2. Find the supplementary angles of the given angles.

(i) 105°

Solution:

180° – 105° = °

(ii) 95°

Solution:

180° - 95° = °

(iii)150°

Solution:

180° - 150° = °

(iv) 20°

Solution:

180° - 20° = °

3. Two acute angles cannot form a pair of supplementary angles. Justify.

Solution:

We know acute angles are angles less than 90°. Supplementary angles are the two angles whose sum would be °.

Since the angles are less than 90°, their sum would never add to 180° and hence two acute angles could never be supplementary.

4. Two angles are equal and supplementary to each other. Find them

Solution:

Two angles are supplementary if their sum is °.

If the two angles are also equal, we can represent each angle as x.

Since they are supplementary:

x + x = °

x = 180°

x = °

Lines and Angles