Exercise 4.7
1 Fill in the blanks
(i) The line which intersects two or more lines at distinct points is called
(ii) If the pair of alternate interior angles are equal then the lines are
(iii) The sum of interior angles on the same side of the transversal are supplementary then the lines are
(iv) If two lines intersect each other then the number of common points they have
2. In the adjacent figure, the lines 'l' and 'm' are parallel and 'n' is a transversal.
Fill in the blanks for all the situations given below
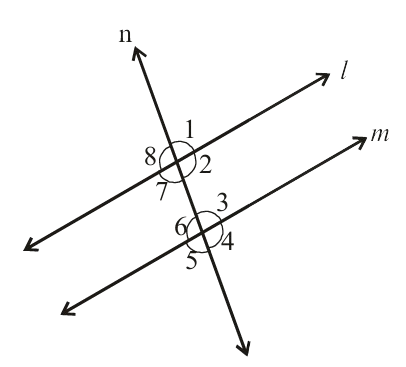
(i)
If ∠1 = 80° then ∠2 = ?
Solution:
∠2 = 180 - 80
=
(ii)
If ∠3 = 45° then ∠7 = ?
Solution:
∠7 =
(iii)
If ∠2 = 90° then ∠8 = ?
Solution:
∠8 =
(iv)
If ∠4 = 100° then ∠8 = ?
Solution:
∠8 =
3. Find the measures of x, y and z in the figure, where l || BC
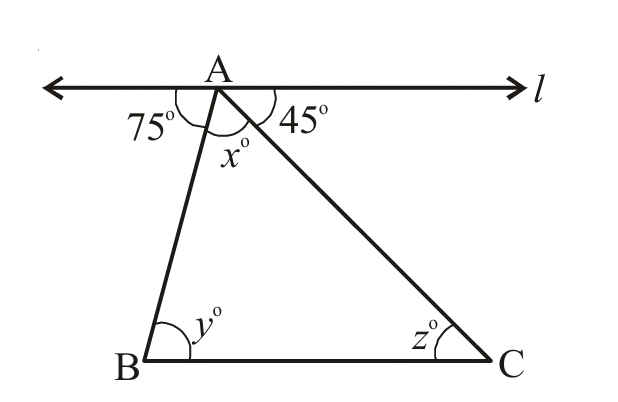
Solution:
∠y =
∠z =
∠x = 180° – (75° + 45°) (angles on
x =
4. ABCD is a quadrilateral in which AB || DC and AD || BC . Find ∠b, ∠c and ∠d.
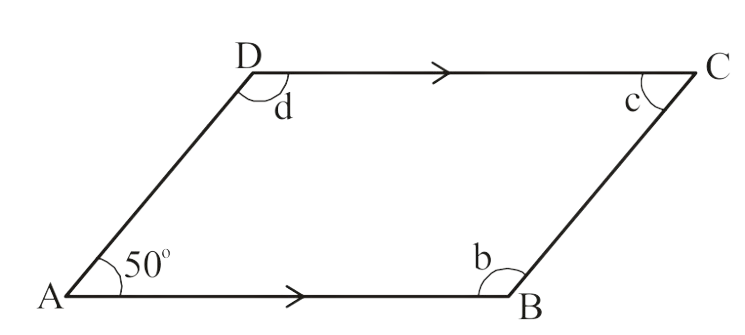
Solution:
ABCD is a parallelogram
So, (i) ∠c =
(ii) ∠b = 180° – 50°
=
(iii) ∠d = ∠b =
5. In a given figure, 'l' and 'm' are intersected by a transversal 'n'. Is l || m ?
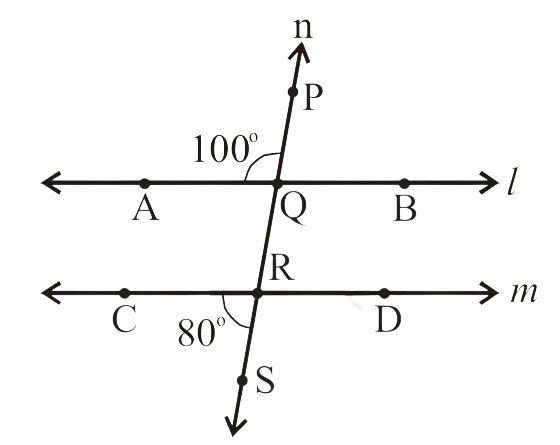
Solution:
∠PQA = 100°
∠PQA + ∠AQR = 180° (Linear Pair)
=> ∠AQR = 180° – 100° =
We are given ∠CRS =
So, ∠CRS = 80° = ∠AQR
∠CRS and ∠AQR are
Since, ∠CRS = ∠AQR corresponding angles are
So, l
