Looking Back
(1) If the sum of two angles is equal to
(2) Each angle in a pair of complementary angles is
(3) If the sum of two angles is equal to
(4) Each angle in a pair of supplementary angles may be either acute or right or obtuse. Two right angles always
(5) The angles formed on both sides of a common arm and a common vertex are
(6) A pair of complementary angles or a pair of supplementary angles need not be adjacent angles.
(7) A pair of angles that are adjacent and supplementary form a
(8) (i)When two lines intersect each other at a point (vertex), the angles formed opposite to each other are called vertically
(ii) A pair of vertically opposite angles are always
(9) (i) A line which intersects two or more lines at distinct points is called a
(ii) A transversal makes
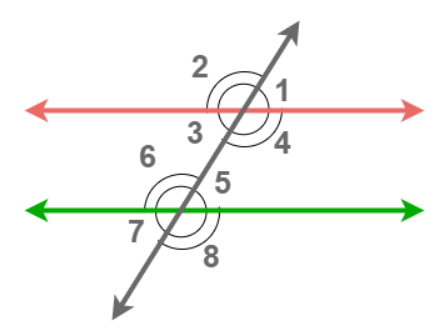
| S.No. | Types of Angles | No. of Pairs | Angles |
|---|---|---|---|
| 1. | Interior angles | — | ∠3, ∠4, ∠5, ∠6 |
| 2. | Exterior angles | — | ∠1, ∠2, ∠7, ∠8 |
| 3. | Vertically opposite angles | 4 pairs | (∠1, ∠3); (∠4, ∠2); (∠5, ∠7); (∠8, ∠6) |
| 4. | Corresponding angles | 4 pairs | (∠1, ∠5); (∠2, ∠6); (∠4, ∠8); (∠5, ∠7) |
| 5. | Alternate interior angles | 2 pairs | (∠3, ∠5); (∠4, ∠6) |
| 6. | Alternate exterior angles | 2 pairs | (∠1, ∠7); (∠2, ∠8) |
| 7. | Interior angles on the same side of transversal | 2 pairs | (∠3, ∠6); (∠4, ∠5) |
(10) When a transversal intersects a pair of parallel lines:
(i) Each pair of corresponding angles are
(ii) Each pair of alternate interior angles are
(iii) Each pair of alternate exterior angles are
(iv) Each pair of interior angles on the same side of the transversal are
