3D Objects Made with Cubes

Visualising Solid Objects

Activity: Let's take some cubes or toy blocks and experiment a bit. Make any random structure (or) arrangement using the toy blocks (try to make an asymmetric one, if possible). Once finished, try to view this structure from different sides. Can you see all the blocks used for making the structure? Especially in the case of an asymmetric random structure, can you guess the number of blocks used for making a structure whilst viewing it only from one side? Even better, ask someone else to view the structure that you have made from just one side and guess the total block number for the structure?

For some simple structures, guessing the answer isn't an issue. However, the more complex the structure becomes, the higher the chances of getting the answer wrong.

(a) Easy to guess the exact number of blocks used

(b) Not so easy to guess the number for making the block castle.

This tells us that, depending on our view point, we perceive the number of blocks used for making a structure differently. Let's take another example as shown below:

Viewed from one angle

Same structure but view point changed. How many squares can be seen now?

While for complex structures, such experiments or activities are liable to cause error. None the less, such visualisation is very helpful. Say, suppose we form a cuboid by putting the small cubes together. Since, the cubes are all symmetric and their dimensions are most likely known by us,we will be able to guess what the length, breadth and height of the cuboid would be.

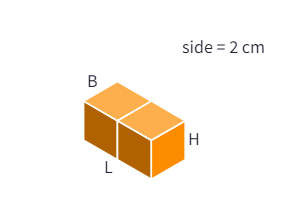
Two cubes froming a cuboid

In the above figure, two cubes are arranged such that a cuboid is now formed as shown? The resulting length is cm, breadth cm and height cm.

Let's Solve

1. Two dice are placed side by side as shown:

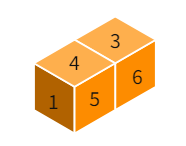
Numerical values denote the number of dots on the face of the die

Can you say what the total would be on the face opposite to

2. Try guessing the number of cubes in the folllowing arrangements: