Number of Faces, Edges and Vertices of Polyhedron

Euler's Relation is a fascinating mathematical formula that establishes a relationship between the number of vertices (V), edges (E), and faces (F) in any convex polyhedron. The formula states:

V - E + F = 2

For a cube:

Vertices (V) = (corner points)

Edges (E) = (lines connecting vertices)

Faces (F) = (square surfaces)

Substituting we get: V - E + F = 8 - 12 + 6 =

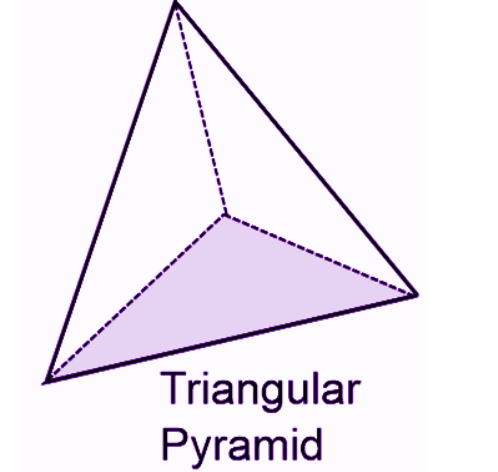
For a triangular pyramid (tetrahedron):

Vertices (V) =

Edges (E) =

Faces (F) =

Substituting we get: V - E + F = 4 - 6 + 4 =

It works for all convex polyhedra (shapes with no indentations or holes). The formula remains true regardless of the polyhedron's size or shape. It doesn't apply to shapes with holes (like a donut shape) or non-convex polyhedra.