Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Co-Ordinate Geometry

    Introduction

    Cartesian System

    Plotting a Point On the Cartesian Plane When Its Co-Ordinates are Given

    Exercise 5.1

    Exercise 5.2

    Exercise 5.3

    Exercise 5.4

    What We Have Discussed

    Enhanced Curriculum Support

    Easy Level Worksheet

    Moderate Level Worksheet

    Hard Level Worksheet

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Co-Ordinate Geometry > Cartesian System

Cartesian System

You have studied the number line in the chapter on ‘Number System’.

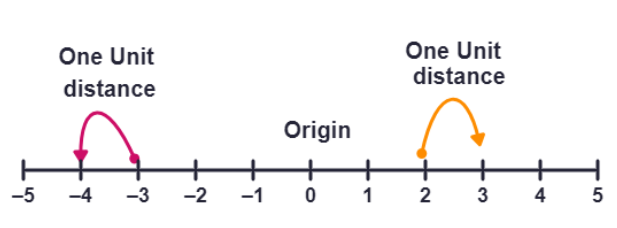
On the number line, distances from a fixed point are marked in equal units positively in one direction and negatively in the other. The point from which the distances are marked is called the .

We use the number line to represent the numbers by marking points on a line at distances.

If one unit distance represents the number ‘1’, then 3 units distance represents the number ‘3’, ‘0’ being at the origin. The point in the positive direction at a distance r from the origin represents the number r.

The point in the negative direction at a distance r from the origin represents the number .

Locations of different numbers on the number line are shown in the below Figure.

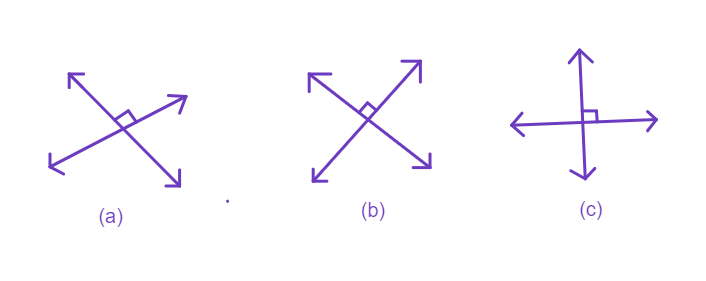
Descartes invented the idea of placing two such lines perpendicular to each other on a plane and locating points on the plane by referring them to these lines. The perpendicular lines may be in any direction such as in the below figure.

But, when we choose these two lines to locate a point in a plane in this chapter, one line will be horizontal and the other will be vertical, as shown.

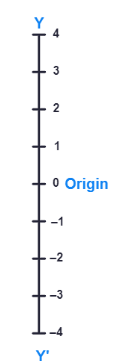
These lines are actually obtained as follows : Take two number lines, calling them X′X and Y′Y. Place X′X horizontal and write the numbers on it just as written on the number line. We do the same thing with Y′Y except that Y′Y is vertical, not horizontal.

Combine both the lines in such a way that the two lines cross each other at their zeroes, or origins. The horizontal line X′X is called the - axis and the vertical line YY′ is called the - axis.

The point where X′X and Y′Y cross is called the origin, and is denoted by .

Since the positive numbers lie on the directions OX and OY, OX and OY are called the directions of the x - axis and the y - axis, respectively.

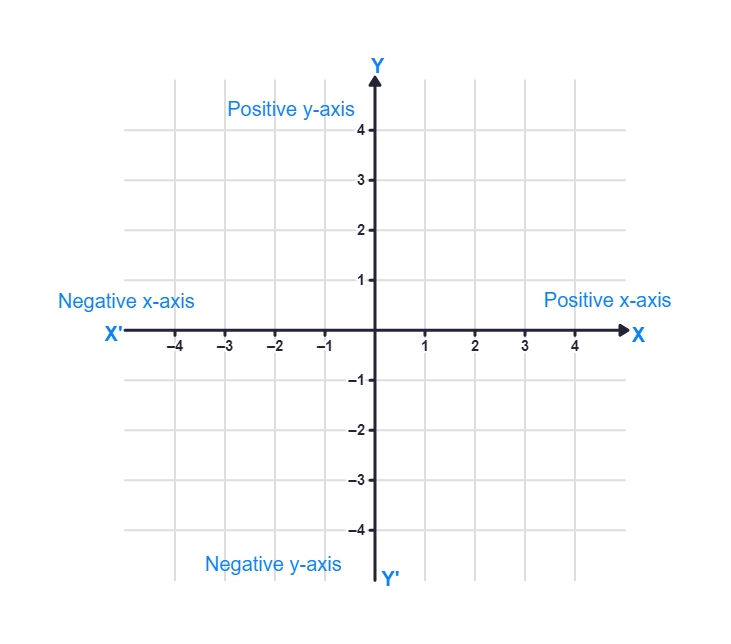
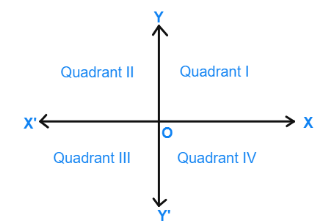
Similarly, OX′ and OY′ are called the directions of the x - axis and the y - axis, respectively.

You observe that the axes (plural of the word ‘axis’) divide the plane into four parts. These four parts are called the quadrants (one fourth part), numbered I, II, III and IV anticlockwise from OX. So, the plane consists of the axes and these quadrants. We call the plane, the Cartesian plane, or the coordinate plane, or the xy-plane. The axes are called the axes.

Now, let us see why this system is so basic to mathematics, and how it is useful. Consider the following diagram where the axes are drawn on graph paper. Let us see the distances of the points P and Q from the axes. For this, we draw perpendiculars PM on the x - axis and PN on the y - axis. Similarly, we draw perpendiculars and as shown.

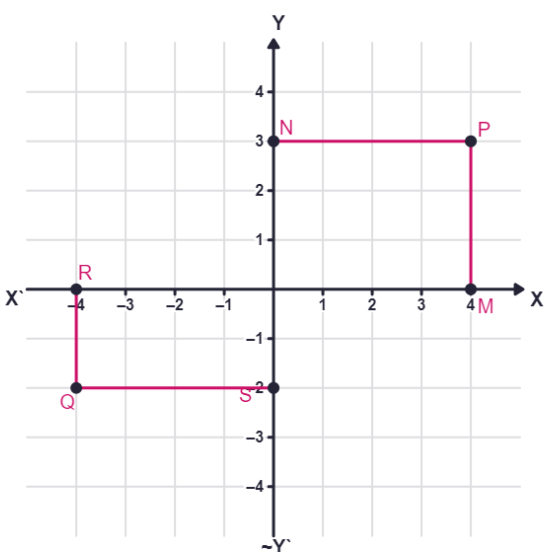
You find that:

(i) The perpendicular distance of the point P from the y - axis measured along the positive direction of the x - axis is PN = OM = units.

(ii) The perpendicular distance of the point P from the x - axis measured along the positive direction of the y - axis is PM = ON = units.

(iii) The perpendicular distance of the point Q from the y - axis measured along the negative direction of the x - axis is OR = SQ = units.

(iv) The perpendicular distance of the point Q from the x - axis measured along the negative direction of the y - axis is OS = RQ = units.

Now, using these distances, how can we describe the points so that there is no confusion?