Plotting a Point On the Cartesian Plane When Its Co-Ordinates are Given

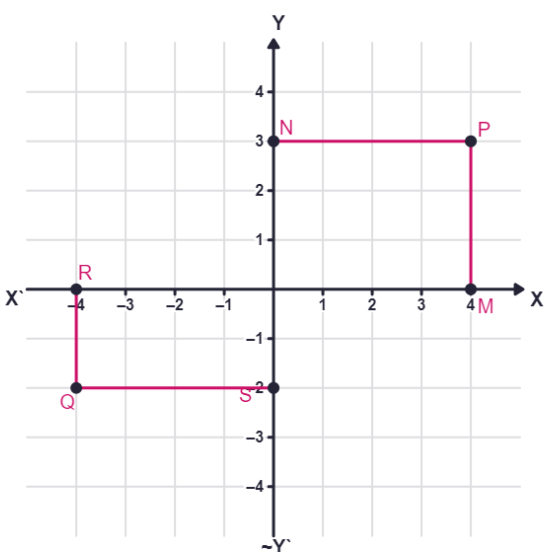
We write the coordinates of a point, using the following conventions:

(i) The x - coordinate of a point is its perpendicular distance from the y - axis measured along the x -axis (positive along the positive direction of the x - axis and negative along the negative direction of the x - axis). For the point P, it is + 4 and for Q, it is – 4. The x-coordinate is also called the abscissaordinate.

(ii) The y - coordinate of a point is its perpendicular distance from the x - axis measured along the y - axis (positive along the positive direction of the y - axis and negative along the negative direction of the y - axis).

For the point P, it is + 3 and for Q, it is –2. The y-coordinate is also called the ordinateabscissa.

(iii) In stating the coordinates of a point in the coordinate plane, the x - coordinate comes first, and then the y - coordinate. We place the coordinates in brackets.

Hence, the coordinates of P are (4, 3) and the coordinates of Q are (– 4, – 2). Note that the coordinates describe a point in the plane uniquely. (3, 4) is not the same as (4, 3).

Continue

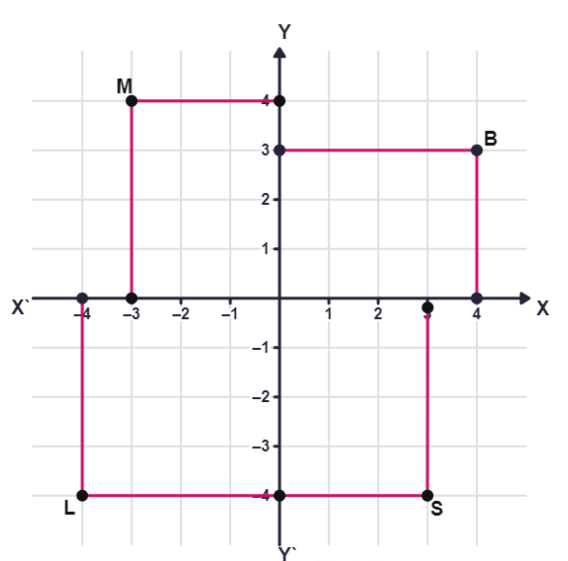
Example 1: See the above fig and complete the following statements:

Solution:

Note: Enter answers in the format- (number,number)

(i) The abscissa and the ordinate of the point B are and , respectively. Hence, the coordinates of B are ().

(ii) The x-coordinate and the y-coordinate of the point M are and , respectively. Hence, the coordinates of M are ().

(iii) The x-coordinate and the y-coordinate of the point L are and , respectively. Hence, the coordinates of L are ( ).

(iv) The x-coordinate and the y-coordinate of the point S are and , respectively. Hence, the coordinates of S are ().

Example 2: Write the coordinates of the points marked on the axes in the given figure.

Solution

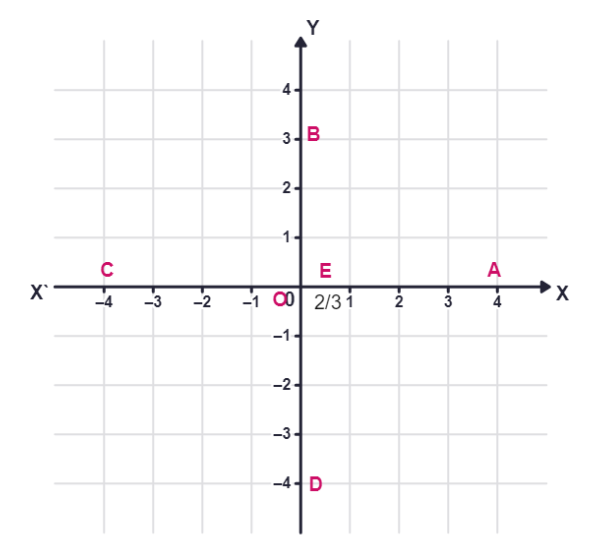
You can see that :

(i) The point A is at a distance of + 4 units from the y - axis and at a distance zero from the x - axis. Therefore, the x - coordinate of A is and the y - coordinate is .

Note: Enter answers in the format- (number,number)

Hence, the coordinates of A are ().

(ii) The coordinates of B are ().

(iii) The coordinates of C are ( ).

(iv) The coordinates of D are ( ).

(v) The coordinates of E are ()

Since every point on the x - axis has no distance (zero distance) from the x - axis, therefore, the y - coordinate of every point lying on the x - axis is always .

Thus, the coordinates of any point on the x - axis are of the form (x, 0), where x is the distance of the point from the y - axis.

Similarly, the coordinates of any point on the y - axis are of the form (0, y), where y is the distance of the point from the x - axis.

What are the coordinates of the origin O? It has zero distance from both the axes so that its abscissa and ordinate are both zero. Therefore, the coordinates of the origin are . (Enter in coordinate system format)

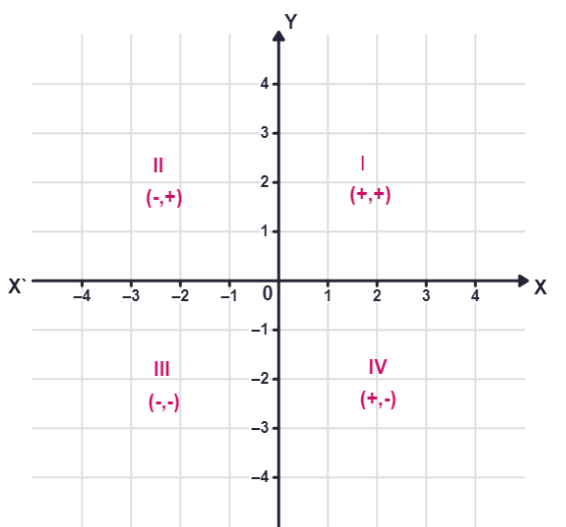
In the examples above, you may have observed the following relationship between the signs of the coordinates of a point and the quadrant of a point in which it lies.

(i) If a point is in the 1st quadrant, then the point will be in the form (+,+)(-,+), since the 1st quadrant is enclosed by the x - axis and the y - axis.

(ii) If a point is in the 2nd quadrant, then the point will be in the form (–,+)(+,-), since the 2nd quadrant is enclosed by the x - axis and the y - axis.

(iii) If a point is in the 3rd quadrant, then the point will be in the form (–,–)(+,+), since the 3rd quadrant is enclosed by the x - axis and the y - axis.

(iv) If a point is in the 4th quadrant, then the point will be in the form (+,–)(-,+), since the 4th quadrant is enclosed by the x - axis and the y - axis.