Enhanced Curriculum Support

SecA

1. Which of the following points lie on the y-axis: A(0,0), B (3,0), C(0,3), D(0,0), E(-5,0), F(0,-1), G(9,0), H(0,-8)

2. The point (0,-4) lies:

(a) On the negative direction of y-axis

(b) in quadrant III

(c) in quadrant IV

(d) On the negative direction of X-axis

3. P(5,-7) is a point on a graph. Draw PM ⊥ y-axis. The coordinates of M are:

(a) On the negative direction of y-axis

(b) in quadrant III

(c) in quadrant IV

(d) On the negative direction of x-axis

4. Find the distance between the points (2, -1) and (-1, 3)

5. Find the distance between the points (0, 5) and (4, 1).

6. Find the coordinates of the midpoint of the line joining (-1, -2) and (3, 4).

7. Find the coordinates of the midpoint of the line segment joining the points (1, 2) and (3, 4).

8. The point on x-axis is: (A) (0, 3) (B) (3, 3) (C) (3, 0) (D) (-3, -3)

9. The equation of x-axis is: (A) y = 0 (B) x = 0 (C) x = y (D) x + y = 0

10. If x > 0 and y < 0, then the point (-x, -y) lies in quadrant. (A) Quadrant III (B) Quadrant IV (C) Quadrant I (D) Quadrant II

SecB

1. Seema has a 10 x 10 kitchen garden attached to her kitchen. She divides it into a 10 x 10 grid and wants to grow some vegetables and herbs in the kitchen. She puts some soil and manure and sows a green chili plant at A, a coriander plant at B and a tomato plant at C. Her friend Khusum visited the garden and praised the plants grown there. She points out that they seem to be in a straight line. Using distance formula or some other method, check if her statement is true.

2. Find the midpoint of the line segment joining the points (-4, 3) and (6, -1).

3. Find the coordinates of the point which divides the line segment joining (2, -3) and (4, 5) in the ratio 1:3.

4. Find the coordinates of the point on the x-axis which is equidistant from the points (1, 2) and (-3, 4).

5. Find the coordinates of the point on the line joining (1, 4) and (5, 12), which divides the segment in the ratio 2:3.

6. Find the length of the diagonal of the rectangle with vertices (2, 3), (6, 3), (6, 7), and (2, 7).

7. Find the coordinates of the point on the line joining (1, 4) and (5, 12), which divides the segment in the ratio 2:3.

8. Plot the points A (2, 1), B (4, 4), C (6, 1) and D (8, 4) in a graph paper, join all the points in order. Find the area of the figure formed.

Sec C

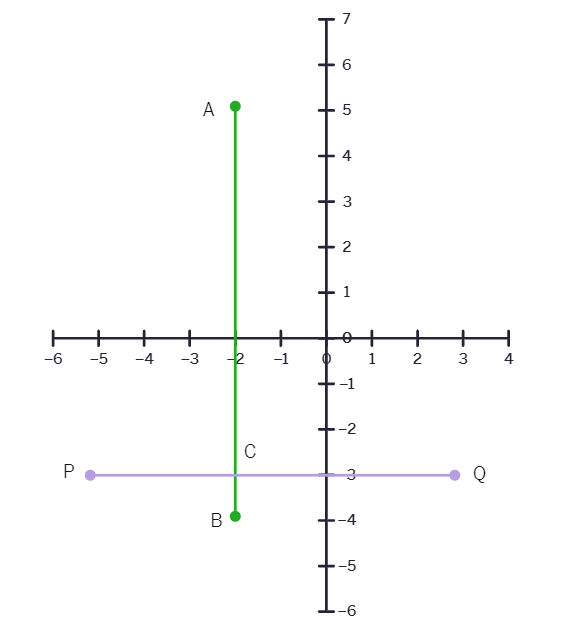
1. Write the equation represented by AB and PQ. Also find the co-ordinates of the their intersection point.

2. Find the distance between the points (3, 2) and (-2, 4), and verify it with the formula.

3. Find the coordinates of the point which divides the line joining (1, 1) and (5, 5) in the ratio 2:3.

4. Find the area of the quadrilateral formed by the points (1, 2), (3, 6), (7, 4), and (5, 1).

5. Find the coordinates of the point that divides the line segment joining (2, 3) and (4, 7) in the ratio 1:2.

6. Find the coordinates of the centroid of the triangle formed by the points A(2, -1), B(4, 3), and C(6, 5).

7. Draw the graph of y = x and y = -x in the same graph. Also find the coordinates of the point where the two lines intersect.

Sec D

1. Find the area of the triangle with vertices A(1, 2), B(4, 6), and C(7, 5) using the determinant method.

2. Find the coordinates of the point that divides the line joining (2, -1) and (5, 3) in the ratio 2:1 and use the section formula to verify.

3. Prove that the points (1, 1), (4, 4), and (7, 7) are collinear using the condition of collinearity.

4. Find the coordinates of the centroid of the triangle formed by the points A(3, 5), B(6, -4), and C(9, 3), and explain the process.

5. Find the distance between the points (2, -1) and (5, 4), and also between (5, 4) and (-1, 2), and check if the points form a right triangle.

6. Find the coordinates of the point on the line joining (2, 3) and (4, 7), which divides the segment in the ratio 3:2, and explain the method used.

7. Find the area of the quadrilateral formed by the points (1, 2), (4, 5), (6, 3), and (3, 1) using the Shoelace Theorem.

8. Find the length of the diagonal of a rhombus with vertices (1, 2), (3, 4), (5, 2), and (3, 0).

9. Find the coordinates of the point which divides the line segment joining (-1, 2) and (7, -3) in the ratio 4:5, and explain the calculation process.

10. Find the area of the triangle formed by the points (2, -3), (4, 6), and (-3, 5) using the coordinate geometry formula.

Problem 1

A farmer discovered an ancient well on his property, marked at coordinates (4, 5). To ensure safety, he decided to build a fence around the well. If the fence needs to be circular and must cover an area of 100 square units, find the equation of the circle that represents the fence. Determine the coordinates of any point on the fence that touches the ground.

Problem 2

During a trekking expedition, a group of students found a steep cliff represented by the line y = 8 on a coordinate grid. They observed a bridge spanning the cliff, starting at (2, 5) and ending at (8, 5). Calculate the length of the bridge and determine the coordinates of its midpoint.

Problem 3

During a cleanliness drive in their locality, students marked four corners of a square garden on a coordinate grid. The coordinates of three corners are (2,3), (6,3), and (6,7). They realized that the fourth corner, (x, y), needs to be determined. If the garden's area represents unity and it must be square-shaped, find the coordinates (x, y) of the fourth corner.

Q1

The vertices of triangle △ABC are A(1, 3), B(4, 6), and C(7, 3). Determine the equation of the perpendicular bisector of side AC. Explain how you can use this perpendicular bisector to verify that △ABC is isosceles.

Q2

A circle with center O and radius 5 units passes through the points (3, 4) and (7, 4). Determine the coordinates of the center O of the circle and write the equation of the circle in standard form. Justify your steps.

Q3

A rectangular garden has one vertex at (2, 3) and diagonally opposite vertex at (8, 7). Determine the coordinates of the other two vertices of the rectangle. Discuss how you can use midpoint formulas and distance formulas to verify your solution.

Questions

1. Abscissa of all the points on the x-axis is:

(A) 0

(B) 1

(C) 2

(D) any number

2. The points whose abscissa and ordinate have different signs will lie in:

(A) I and II quadrants

(B) II and III quadrants

(C) I and III quadrants

(D) II and IV quadrants

Solve the below questions given below

3. Without plotting the points indicate the quadrant in which they will lie, if:

(i) ordinate is 5 and abscissa is – 3

(ii) abscissa is – 5 and ordinate is – 3

(iii) abscissa is – 5 and ordinate is 3

(iv) ordinate is 5 and abscissa is 3

4. Plot the following points and write the name of the figure obtained by joining them in order: P(– 3, 2), Q (– 7, – 3), R (6, – 3), S (2, 2)

5. In the figure, LM is a line parallel to the y-axis at a distance of 3 units.

(i) What are the coordinates of the points P, R and Q?

(ii) What is the difference between the abscissa of the points L and M?

6. Write the coordinates of the vertices of a rectangle whose length and breadth are 5 and 3 units respectively, one vertex at the origin, the longer side lies on the x-axis and one of the vertices lies in the third quadrant.

7. Three vertices of a rectangle are (3, 2), (– 4, 2) and (– 4, 5). Find the coordinates of the fourth vertex.

8. Plot the points A (1, – 1) and B (4, 5). (i) Draw a line segment joining these points. Write the coordinates of a point on this line segment between the points A and B. (ii) Extend this line segment and write the coordinates of a point on this line which lies outside the line segment AB.

Q1

Imagine a town planning committee is designing a new park. The park is in the shape of a triangle with vertices at coordinates A(−3,2), B(1,−4), and C(x,y). The committee wants to place a fountain at point F inside the park such that the distances from F to the vertices A, B, and C are equal.

1. Determine the coordinates (x,y) of vertex C such that triangle ABC is isosceles with AB = AC.

2. Suppose the committee decides to plant trees along the sides of △ABC. Determine the coordinates of the midpoint of side AB to optimize tree placement.

3. If the area of △ABC is 24 square units, find the coordinates of the centroid G of the triangle.

Sol 1

Let's solve each part of the question step by step:

1. Determine the coordinates (x,y) of vertex C such that triangle ABC is isosceles with AB = AC.

For triangle ABC to be isosceles with AB = AC, point C must be equidistant from points A and B. This means C lies on the perpendicular bisector of AB.

Calculate the midpoint of AB:

Midpoint of AB = (−3+12, 2−42) = (−1,−1)

Find the equation of the perpendicular bisector of AB, which passes through the midpoint (−1,−1) and has a slope perpendicular to AB.

Slope of AB = −4−21+3 = −64 = −32

Thus, slope of perpendicular bisector = 23

Using the point-slope form:

y+1=23x+1

y=23x−13

Distance formula for AC: AC = x+32+y−22

Distance formula for AB: AB = 1−−32+−4−22 = 42+−62

= 16+36 = 52 = 213

Since, we need AC = AB

x+32+y−22 = 213

Substitute y value into the equation and square both sides to remove the roots.

x+32+23x−732 = 52

Upon expanding and simplifying:

9x2+6x+9+4x2−14x+49=468

13x2+40x−338=0

Finding the roots of the above equation in the formula −b±b2−4ac2a,

we get x = 3.78 and -6.86 (ignore negative value as location coordinates in a park can't be negative)

Putting x = 3.78 in equation for y: y = 233.78−13 = 2.19

Therefore, the coordinates of vertex C are approximately (3.78,2.19). These coordinates satisfy the condition that triangle ABC is isosceles with AB = AC.

2. The midpoint M of AB is already calculated: M = (−1,−1)

3. The centroid G divides each median of the triangle in a 2:1 ratio from the vertex.

Calculate the coordinates of the centroid G:

G(x) = x1+x2+x33 and G(y) = y1+y2+y33

Substituting A(−3,2), B(1,−4), C(x,y): ​ G(x) = −3+1+x3 = x−23 -(A) ​ G(y) = 2−4+y3 = y−23 - (B)

Also given Area of triangle = 12x1y2−y3+x2y3−y1+x3y1−y2 = 24

Substituting A(−3,2), B(1,−4), C(x,y):

48 = 15 + 3y + 6x - (C)

Now, solve for x and y using the above equation and the condition that F (the point where distances to vertices are equal) is at the centroid G:

x−23 = y−23

x = y

Putting this in eqn(C) :

48 = 15 + 9x

x = 339 = 113

Since y = x, we have x = 113 and y = 113.

​Putting this in eqn (A) and (B):

G(x) = 59 and G(y) = 59