Criteria for Congruence of Triangles
Let us recall the four criteria for congruence of triangles and use those criteria to prove mathematical statements.
Think: Equality of one pair of sides or one pair of sides and one pair of angles is
As it turns out, the equality of just one pair of adjacent sides (or) a pair of angles isn't enough to guarantee congruency between two triangles.
However, upon comparing a bunch of congruent triangles, we make an observation that the equality of two sides and the included angle is enough to prove the congruence of two triangles.
This is where we get the first criterion for the congruency of triangles.
Axiom (SAS congruence rule)
Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
Since, this result cannot be proved with the help of any previously known results, it is accepted as an
As mentioned earlier, the included angles needs to be in between the two equal/congruent sides for there to be congruency.
This is why, SAS congruence rule holds while rules like ASS or SSA do not.
We make another observation that the equality of two angles and the included side is also sufficient for the congruence of triangles.
This gives us the Angle-Side-Angle criterion for triangle congruency which is written as ASA criterion in short hand.
Since this result can be proved using the SAS axiom, it is called a
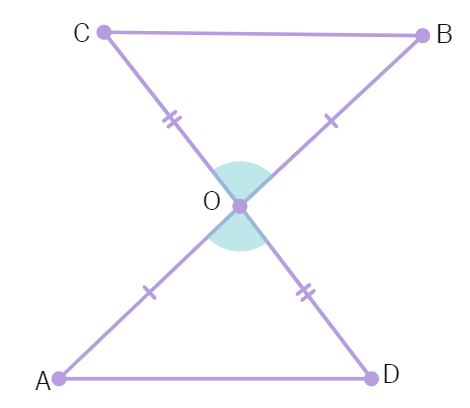
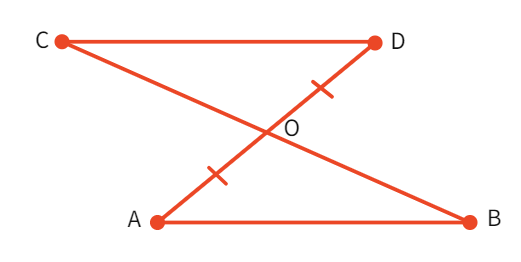
Example 1 : In the below figure, OA = OB and OD = OC. Show that:
(i) ∆ AOD ≅ ∆ BOC and (ii) AD || BC
Solution:
(i) Consider the triangles ∆ AOD and ∆ BOC:
We have been given: OA =
Also, since ∠ AOD and ∠ BOC form a pair of
So, ∆ AOD ≅ ∆
(ii) In congruent triangles AOD and BOC, the other corresponding parts are also
So, ∠ OAD = ∠
Therefore, AD || BC.
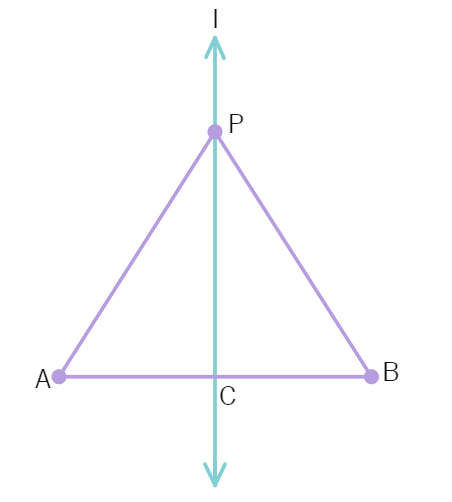
Example 2 : AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
Solution :
Line l ⊥ AB and passes through C which is the
Considering the triangles ∆ PCA and ∆ PCB:
AC =
∠ PCA = ∠ PCB =
PC =
So, ∆ PCA ≅ ∆
Thus, by CPCT: PA =
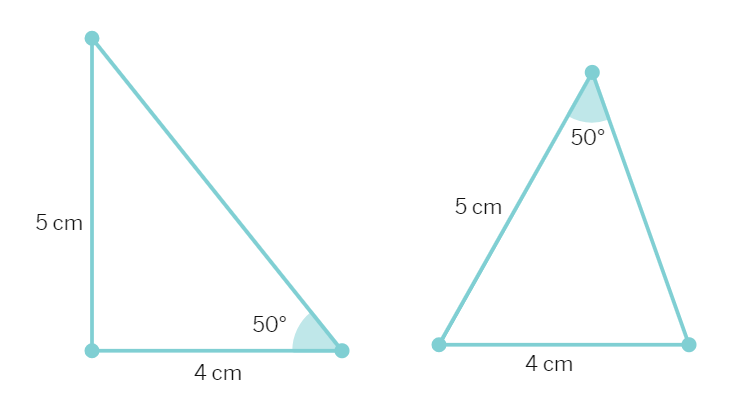
Now, let us construct two triangles, whose sides are 4 cm and 5 cm and one of the angles is 50° and this angle is not included in between the equal sides. Are the two triangles congruent?
Try to repeat this activity with more pairs of triangles.
You will observe that for triangles to be congruent: it is very important that the equal angles are included between the pairs of equal sides.
So, SAS congruence rule holds but not ASS or SSA rule.
Next, try to construct the two triangles in which two angles are 60° and 45° and the side included between these angles is 4 cm.
Cut out these triangles and place one triangle on the other. What do you observe?
We see that one triangle covers the other completely; that is, the two triangles are
Repeat this activity with more pairs of triangles. You will observe that equality of two angles and the included side is
This result is the Angle-Side-Angle criterion for congruence and is written as ASA criterion.
Since this result can be proved, it is called a theorem and to prove it, we use the SAS axiom for congruence.
Theorem (ASA congruence rule) : Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
Proof: Considering the two triangles ABC (Fig B) and DEF (Fig A) in which:
∠ B = ∠ E, ∠ C = ∠ F and BC = EF
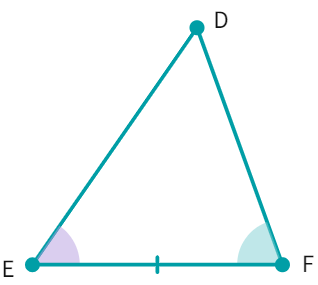
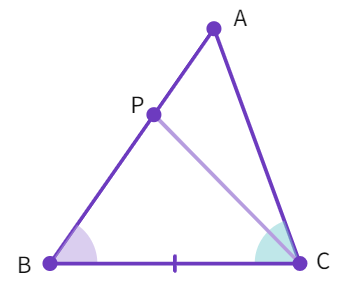
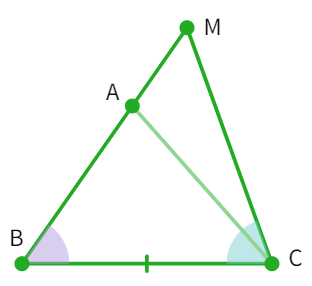
Now we are required to prove that:
∆ ABC ≅ ∆ DEF
For proving the congruency between the two triangles, we need to tackle three different cases:
AB = DE
AB > DE
AB < DE
Case (i) : Assume AB = DE
- Considering the triangles ∆ ABC and ∆ DEF, we get: AB = DE (Assumed), ∠ B = ∠
(Given), BC = (Given) - So, by
congruency rule: ∆ ABC ≅ ∆ - Hence, the above assumption is true.
Looking at the second case.
Case (ii): Assuming that AB > DE.
- Let's take a point P on AB such that PB = DE.
- Considering the triangles ∆ PBC and ∆ DEF,we will now get: PB =
(By construction) - ∠ B = ∠
(Given) and BC = (Given) - Using
congruency axiom: ∆ PBC ≅ ∆ - Since the triangles have been proven to be congruent, their corresponding parts will also have to be
. - Thus, ∠ PCB = ∠
- We have already been given that: ∠
= ∠DFE - Thus, ∠ACB has to be equal to ∠PCB which will be possible only if point P
with point A. - Hence, the above assumption is false.
Case (iii): If we assume AB < DE.
- let a point M be on DE such that MB = DE.
- Consider the triangles ∆ MBC and ∆ DEF: MB = DE (By construction)
- Also, ∠B = ∠
and BC = (Given) - Using
congruency axiom we get: ∆ MBC ≅ ∆ - Since the triangles have been proven to be congruent, their corresponding parts will also be equal. Thus, ∠ MCB = ∠
- Like earlier this can only be possible if point M and point A
. - Hence, the above assumption is false.
Thus,
AB = DE.
Now, consider two triangles where two pairs of angles and one pair of corresponding sides are equal but the side is not included between the equal pair of angles. Are the triangles still congruent in this case? As it turns out - they will be congruent.
We know that:
The sum of the three angles of a triangle is 180°.
So, if two pairs of angles are equal, the third pair will also be
as the measure of both the corresponding angles will be (180° – sum of equal angles).
So we can conclude that when if any two pairs of angles and one pair of corresponding sides are equal, the triangles are congruent. We call this as the AAS Congruence Rule.
Theorem(AAS congruence rule) : Two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal
Note: For congruency, equality of all three angles is not sufficient for congruence of triangles. The length of the sides involved are also important. Thus, out of the three equal parts, one has to be a side.
Example 3: Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD. Show that:
(i) ∆AOB ≅ ∆DOC
(ii) O is also the mid-point of BC
- Consider the triangles ∆ AOB and ∆ DOC: ∠ABO =∠
as they are interior angles with AB || CD and as the transversal - Also, ∠AOB = ∠
as they are vertically opposite angles and OA = (Given) - Therefore, by
congruency rule: ∆AOB ≅ ∆ - Since, the corresponding parts of the triangles will be equal: OB =
- Meaning O is the mid-point of
- Hence, proved.
