Enhanced Curriculum Support
This is a comprehensive educational resource designed to provide students with the tools and guidance necessary to excel. This support system is structured to cater to various aspects of learning, ensuring that students are well-prepared for academic challenges and practical applications of mathematical concepts. Some are the key benefits are mentioned below:
1.Comprehensive Learning: This holistic approach helps students gain a thorough understanding of the subject. Practical Application: The resources encourage students to apply mathematical concepts to real-life scenarios, enhancing their practical understanding and problem-solving skills.
2.Critical Thinking and Reasoning: Value-Based and HOTS questions promote critical thinking and reasoning abilities. These skills are crucial for students to tackle complex problems and make informed decisions.
3.Exam Preparedness: Sample Question Papers and NCERT Exemplar Solutions provide ample practice for exams. They help students familiarize themselves with the exam format and types of questions, reducing exam anxiety.
4.Ethical and Moral Development: Value-Based Questions integrate ethical and moral lessons into the learning process, helping in the overall development of students' character and social responsibility. By incorporating these diverse elements, Enhanced Curriculum Support aims to provide a robust and well-rounded knowledge, preparing students for both academic success and real-world challenges.
Sample Question Papers
Sec A
1.In the adjoining figure, B = C and AD BC. The rule by which △ABD ≅ △ADC:
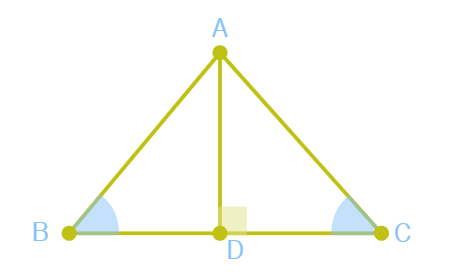
(a) SSS (c) RHS (b) SAS (d) AAS
2.Assertion (A): The side of an equilateral triangle is 6 cm then the area of the triangle is 9
Reason (R): All the sides of an equilateral triangle are equal.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
3.If the sides of a triangle are produced in order, then the sum of the three exterior angles so formed is:
(a) 90° (c) 180°
(b) 270° (d) 360°
4.In the adjoining figure, BC = AC. If ∠ACD = 115°, the ∠ A is :
(a) 50° (b) 65° (c) 57.5° (d) 70°
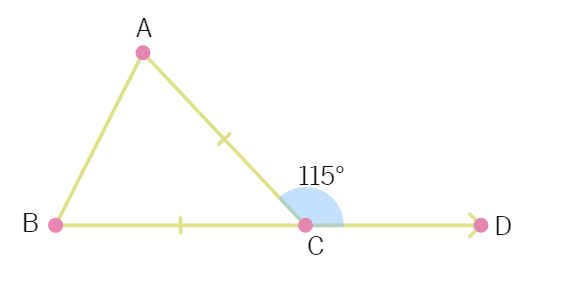
5.The side BC of ABC is produced to a point D. The bisector of ∠A meets side in L. If ∠ABC = 30° and ∠ACD = 115°, then ∠ALC = ?:
(a) 85° (b) None of these (c) 145° (d) 72
5.Assertion (A): The sides of a triangle are in the ratio of 25 : 14 : 12 and its perimeter is 510 cm. Then the area of the triangle is 4449.08
Reason (R): Perimeter of a triangle = a + b + c, where a, b, c are sides of a triangle.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) R is not the correct explanation of A.
(d) A is false but R is true.
6.Assertion (A): In ABC, E and F are the midpoints of AC and AB respectively. The altitude AP at BC intersects FE at Q. Then, AQ = QP.
Reason (R): Q is the midpoint of AP.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
7.In figure, what is the value of x ?
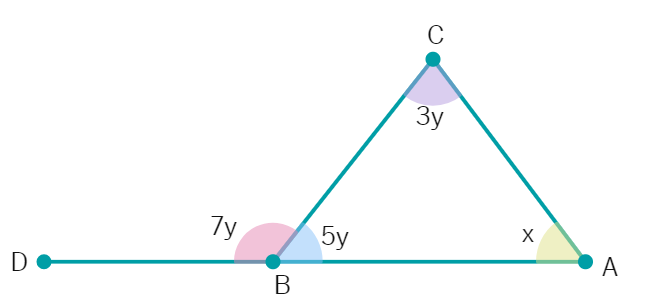
(a) 60 (c) 45 (b) 35 (d) 50
8.Assertion (A): The perimeter of a right angled triangle is 60 cm and its hypotenuse is 26 cm. The other sides of the triangle are 10 cm and 24 cm. Also, area of the triangle is 120
Reason (R):
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false
(d) A is false but R is true.
9.In a △ABC, if A = 60°, B = 80° and the bisectors of B and C meet at O, the BOC = ?:
(a) 60° (c) 150° (b) 30° (d) 120°
10.In the adjoining figure, AB = FC, EF = BD and AFE = CBD. Then the rule by which △AFE ≅ △CBD:
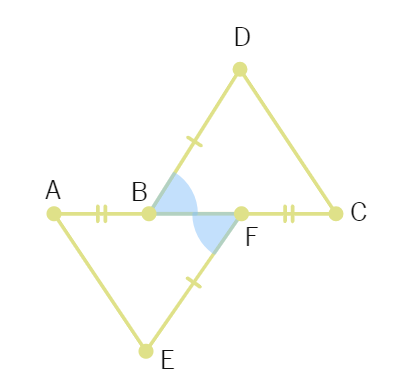
(a) SSS (c) ASA (b) AAS (d) SAS
Sec B
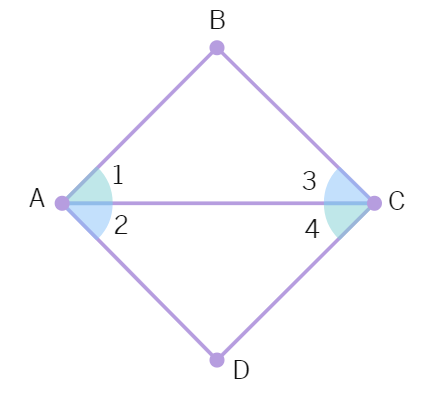
1.In the given figure, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C.
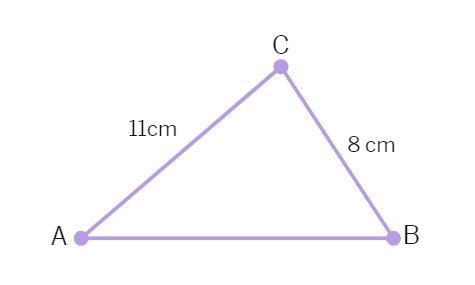
2.Find the area of a triangle, two sides of which are 8 cm and 11 cm and the perimeter is 32 cm.
3.The perimeter of an equilateral triangle is 60 cm. Find its height. (Given:
4.On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
5.The height of an equilateral triangle measures 9 cm. Find its area, correct to 2 places of decimal. (Take
Sec C
1.ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Then prove that:
(i) D is the midpoint AC
(ii) MD is perpendicular to AC
(iii) CM = AM =
2.If two isosceles triangles have a common base, prove that the line joining their vertices bisects them at right angles.
3.S is any point on side QR of a △PQR. Show that: PQ + QR + RP > 2PS.
4.The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3: 2. Find the area of the triangle.
5.The perimeter of a triangle is 480 meters and its sides are in the ratio of 1 : 2 : 3. Find the area of the triangle?
6.BN and CM are perpendiculars to a line passing through the vertex A of a triangle ABC. If L is the mid point of BC, Prove that LM = LN.

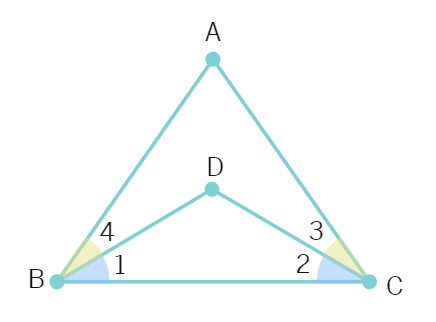
7.In the above given figure, we have ∠ABC = ∠ACB , ∠4 = ∠3. Show that: ∠1 = ∠2.
Sec D
1.In a forest, a big tree got broken due to heavy rain and wind. Due to this rain the big branches AB and AC with lengths 5m fell down on the ground. Branch AC makes an angle of 30° with the main tree AP. The distance of Point B from P is 4 m. You can observe that ABP is congruent to ACP.


(i) Show that △ACP and △ABP are congruent.
(ii) Find the value of ∠ACP ?
(iii) Find the value of ∠BAP ?
2.As shown In the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length. Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles. This time electricians need a staircase of 10 m so that it can reach at point P on the pole and this should make 60° with line AC.
(i) Show that ΔAPC and ΔBPC are congruent.
(ii) Find the value of ∠x.
(iii) What is the value of ∠PBC ?
(or)
Find the value of ∠y.

3.Haresh and Deep were trying to prove a theorem. For this they did the following:
(i) Draw a triangle ABC
(ii) D and E are found as the mid points of AB and AC
(iii) DE was joined and DE was extended to F so DE = EF
(iv) FC was joined.
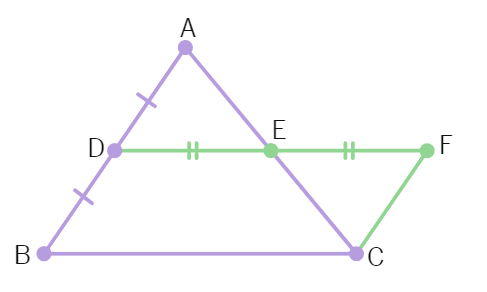
(a) △ADE and △EFC are congruent by which criteria?
(b) Show that CF ∥ AB.
(c) Show that CF = BD.
(OR)
Show that DF = BC and DF ∥ BC.
4.There is a Diwali celebration in the DPS school Janakpuri New Delhi. Girls are asked to prepare Rangoli in a triangular shape. They made a rangoli in the shape of triangle ABC. Dimensions of △ABC are 26 cm, 28 cm, 25 cm.
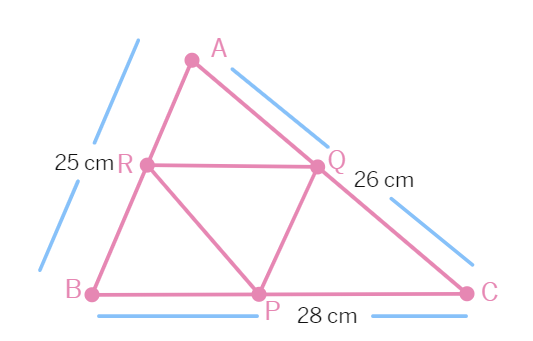
(i) In fig R and Q are mid-points of AB and AC respectively. Find the length of RQ.
(ii) Find the length of Garland which is to be placed along the side of △QPR.
(iii) R, P and Q are the mid-points of AB, BC, and AC respectively. Then find the relation between area of △PQR and area of △ABC.
(OR)
R, P, Q are the mid-points of corresponding sides AB, BC, CA in △ABC, then name the figure so obtained BPQR.
Value Based Questions
Problem 1
A city planning committee is constructing triangular-shaped parks and walkways, ensuring that each park is symmetrical and stable using isosceles and equilateral triangles. The design is inspired by nature, which often uses triangular shapes for balance and strength, such as in mountains or leaves.
How do isosceles and equilateral triangles in these constructions reflect respect for nature’s design? Why is it important to incorporate such natural designs in urban planning?
Problem 2
In a school project, a group of students is tasked with designing triangular garden patches for a community garden. The students need to ensure that the garden patches are not only symmetrical but also aesthetically pleasing. They decide to use the criteria of congruence (SSS, SAS, ASA, RHS) to create their designs.
How can the students use the concept of triangle congruence to ensure that all the triangular patches are identical? How does working together and following a common method reflect the value of teamwork?
Problem 3
A group of students is trying to solve a complex problem involving the Midpoint Theorem in triangles. After several attempts and failures, they finally manage to prove the theorem using logical steps. Despite facing difficulties, they didn’t give up.
How does their approach reflect the value of perseverance in solving problems, both in mathematics and in real-life challenges? Why is it important to keep trying even when the solution isn’t immediately clear?
HOTS
Q1
Given a triangle △PQR, the midpoints of sides PQ and PR are M and N, respectively. Prove that MN is parallel to QR and MN is half the length of QR (Midpoint Theorem). Now extend this concept to quadrilaterals by finding if a similar relationship holds in any quadrilateral.
Q2
Two triangles are congruent by the SSS criterion. In one triangle, two sides are known as 5 cm and 7 cm, while the third side is unknown. In the second triangle, two sides are known as 8 cm and 12 cm, and the third side is also unknown. Find the possible lengths of the unknown sides in both triangles and prove that the two triangles can still be congruent.
Q3
In triangle ABC, AB = AC and angle BAC = 40°. A point D is taken on AC such that BD is perpendicular to AC. Prove that triangle ABD is not an equilateral triangle, and explain why equality cannot hold between sides AB, BD, and AD using properties of triangles.
NCERT Exemplar Solutions
Choose the correct option
Questions
If ∆ ABC ≅ ∆ PQR and ∆ ABC is not congruent to ∆ RPQ, then which of the following is not true:
(A) BC = PQ (B) AC = PR
(C) QR = BC (D) AB = PQ
If AB = QR, BC = PR and CA = PQ, then:
(A) ∆ ABC ≅ ∆ PQR (B) ∆ CBA ≅ ∆ PRQ
(C) ∆ BAC ≅ ∆ RPQ (D) ∆ PQR ≅ ∆ BCA
In ∆ ABC, BC = AB and ∠B = 80°. Then ∠A is equal to:
(A) 80° (B) 40°
(C) 50° (D) 100°
D is a point on the side BC of a ∆ ABC such that AD bisects ∠BAC. Then:
(A) BD = CD (B) BA > BD
(C) BD > BA (D) CD > CA
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be:
(A) 3.6 cm (B) 4.1 cm
(C) 3.8 cm (D) 3.4 cm
In ∆ PQR, if ∠R > ∠Q, then:
(A) QR > PR (B) PQ > PR
(C) PQ < PR (D) QR < PR
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are:
(A) isosceles but not congruent (B) isosceles and congruent
(C) congruent but not isosceles (D) neither congruent nor isosceles
Answer the given below questions
Questions
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
In ∆ PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
Q is a point on the side SR of a ∆ PSR such that PQ = PR. Prove that PS > PQ.
S is any point on side QR of a ∆ PQR. Show that: PQ + QR + RP > 2 PS.
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
ABC and DBC are two triangles on the same base BC such that A and D lie on the opposite sides of BC, AB = AC and DB = DC. Show that AD is the perpendicular bisector of BC.
Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
In a right triangle, prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse.
AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
ABC is a right triangle such that AB = AC and bisector of angle C intersects the side AB at D. Prove that AC + AD = BC.
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than
In a triangle ABC, D is the mid-point of side AC such that BD =
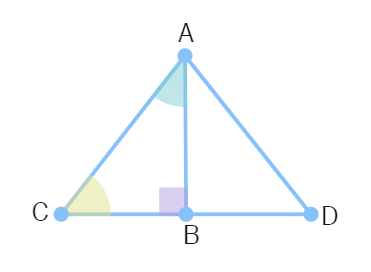
In the figure, ABC is a right triangle and right angled at B such that ∠BCA = 2 ∠BAC. Show that hypotenuse AC = 2 BC.
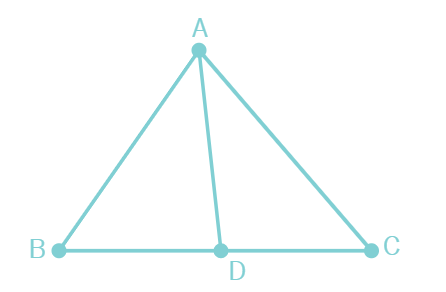
In the figure, AD is the bisector of ∠BAC. Prove that AB > BD.
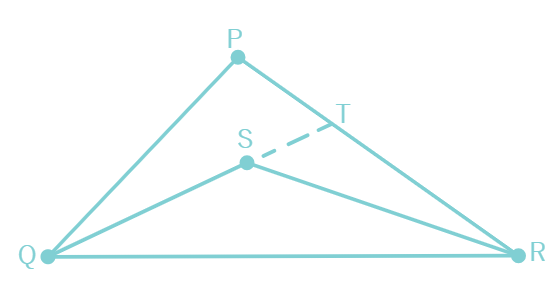
S is any point in the interior of ∆ PQR. Show that SQ + SR < PQ + PR.
If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.
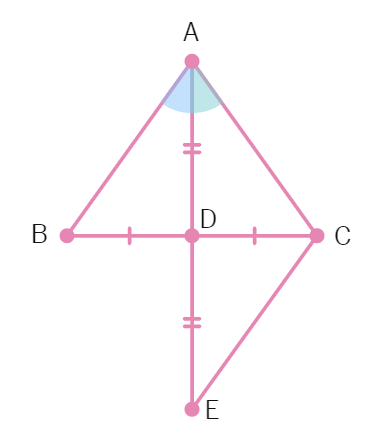
In the figure, PQ > PR and QS and RS are the bisectors of ∠Q and ∠R, respectively. Show that SQ > SR.
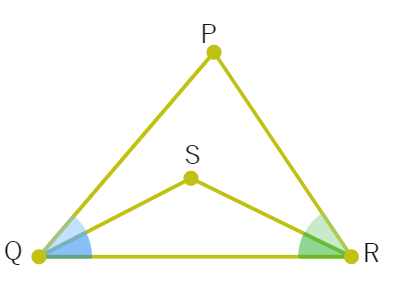
CDE is an equilateral triangle formed on a side CD of a square ABCD (as shown in below figure). Show that ∆ ADE ≅ ∆ BCE.
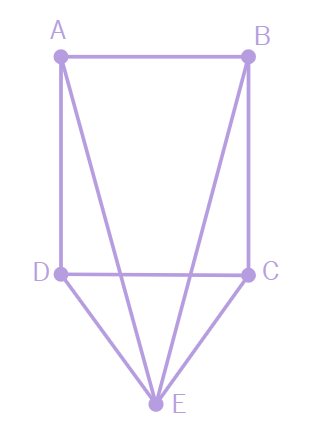
In the below figure, two lines AB and CD intersect each other at the point O such that BC || DA and BC = DA. Show that O is the midpoint of both the line-segments AB and CD.

Case Based Questions
Q1
In a town, two tall buildings are built on the same ground level. An engineer notices that the angle of elevation from the top of a 12-meter high building to the top of a 24-meter high building is 30°. The distance between the two buildings is 10 meters.
Prove that the two triangles formed by the engineer’s line of sight are similar.
Using the properties of similar triangles, find the height of a third building located between the two, such that the angle of elevation from the top of the shorter building is 20° and from the top of the taller building is 10°.
If the distance between the third building and the two others is proportional to their heights, calculate this distance.
Q2
A land surveyor is measuring distances between various points on a plot of land. He finds that two triangular sections of land have sides in the ratio 3 : 4 : 5 and 6 : 8 : 10 respectively. He needs to verify if the two triangular sections are congruent to assess the shape of the plot.
Are the two triangular sections congruent? Justify your answer using the criteria for congruence of triangles.
If they are congruent, what conclusion can be drawn about the land’s boundary?
If one of the triangles is rotated, will it still remain congruent to the other triangle? Why?
Q3
A triangular garden has sides measuring 6 meters, 8 meters, and 10 meters. A gardener wishes to plant trees at the vertices of the triangle. He also wants to create smaller triangular flower beds inside the garden such that each of the smaller triangles is similar to the larger one.
Prove that the triangle is a right-angled triangle.
How would you design the smaller triangles so that they are similar to the larger one? Justify your reasoning using properties of similar triangles.
If the gardener wants to divide the garden into two smaller triangular sections similar to the original, what would be the ratio of the sides of these smaller triangles to the original triangle?
