Exercise 7.1

1.In quadrilateral ACBD, AC = AD and AB bisects ∠ A. Show that ∆ ABC ≅ ∆ ABD. What can you say about BC and BD?

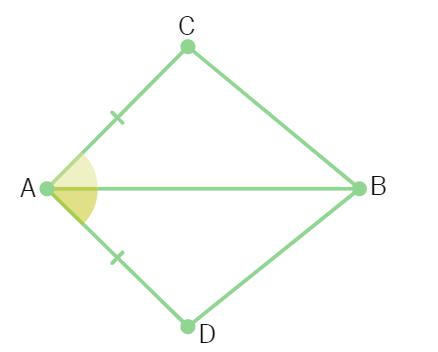
Solution:

Instructions

In quadrilateral ACBD, we have: AC = and being the bisector of ∠A.

In ∆ABC and ∆ABD: AC = AD (Given) and ∠ CAB = ∠ ( as AB bisects ∠ CAB)

We also have: AB = ( Side)

Thus, ∆ ABC ≅ ∆ (By congruence axiom)

By CPCT: BC = .

Hence, proved.

2. ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA as shown below. Prove that:

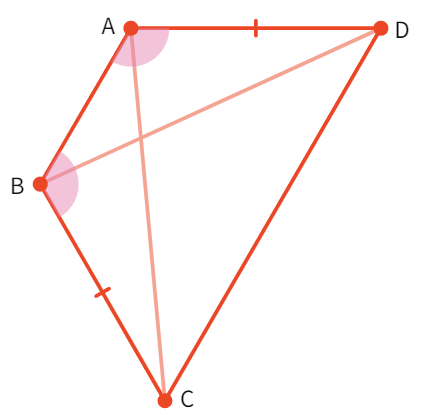
(i) ∆ ABD ≅ ∆ BAC

(ii) BD = AC

(iii) ∠ ABD = ∠ BAC

Instructions

Prove the above statements

Given that: ∠DAB = ∠ and AD =
Consider the triangles ΔABD and ΔBAC:
AB = (common arm), ∠ DAB = ∠CBA and AD = BC (given)
By congruency rule, ΔABD ≅ Δ
By CPCT: BD = and ∠ ABD = ∠
Hence, proved.

AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.

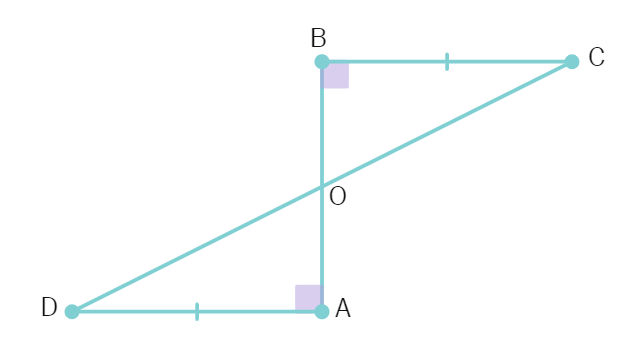
Solution:

Instructions

In ∆BOC and ∆AOD, we have: ∠BOC = ∠ while BC = (Given data)

∠BOC = ∠ ( opposite angles) (Check the angles)

Thus, ∆OBC ≅ ∆ (By congruency rule)

⇒ By CPCT: OB = i.e., O is the mid-point of AB. Thus, CD AB.

l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that ∆ ABC ≅ ∆ CDA.

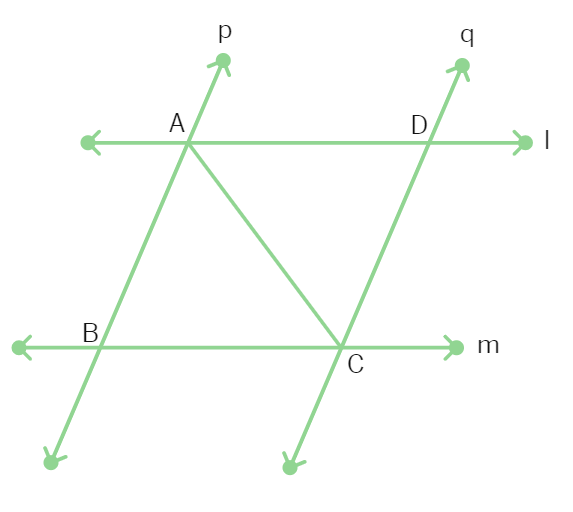
Solution:

Instructions

From the figure: p || and AC is a .

This gives us: ∠BAC = ∠ …(1) (as they are angles)

We also have: l || with AC again, as a transversal which gives us ∠BCA = ∠ …(2) (as they are angles)

Considering ∆ABC and ∆CDA: ∠BAC = ∠ and CA = ( side)

Further, ∠BCA = ∠.

Therefore, ∆ABC ≅ ∆ (By congruency rule)

5.Line l is the bisector of an angle ∠ A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠ A. Show that:

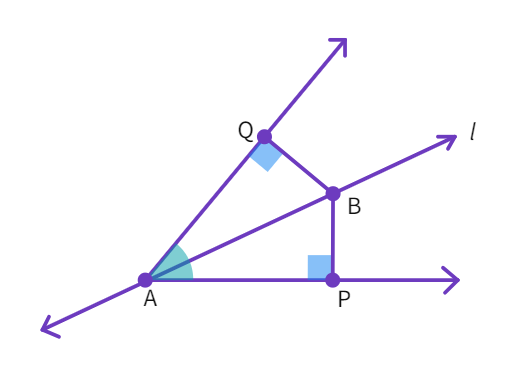
(i) ∆ APB ≅ ∆ AQB

(ii) BP = BQ

Instructions

Prove the above statements

Considering the triangles ΔAPB and ΔAQB: ∠P = ∠ (both are angles)
AB = (common arm), ∠ BAP = ∠ (Line l is the of angle A)
By congruency rule, ΔAPB ≅ Δ
By CPCT: BP = . In other words, the point B is from the arms of ∠A.
Hence, proved.

6.In the below figure we have been given that AC = AE, AB = AD and ∠ BAD = ∠ EAC. Show that BC = DE.

Instructions

Prove the above statement

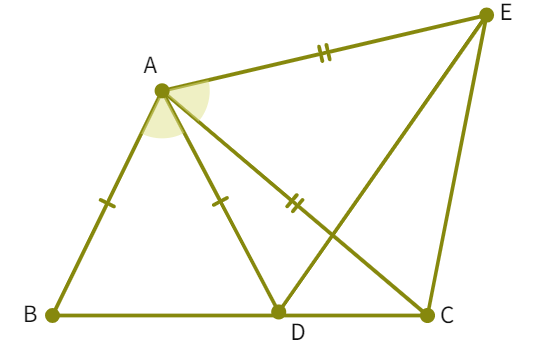
Given: ∠BAD = ∠CAE. If we add ∠DAC on both sides, we get: ∠BAD + ∠DAC = ∠CAE + ∠DAC i.e. ∠ = ∠
Considering the triangles ΔABC and ΔADE: AC = (given)
Also, ∠BAC = ∠DAE (proven) and AB = (given)
Thus, by congruency rule: ΔABC ≅ Δ
By CPCT: BC =
Hence, proved.

7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB as shown. Prove that:

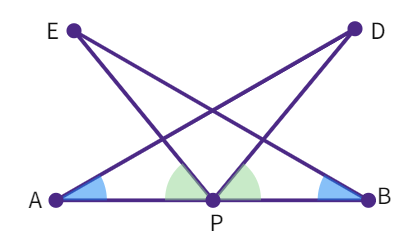
(i) ∆ DAP ≅ ∆ EBP

(ii) AD = BE

Instructions

Prove the above statements

Given: P is the mid-point of line segment AB i.e. AP = . Also given: ∠BAD = ∠ABE and ∠EPA = ∠DPB
In ∠EPA = ∠DPB, adding ∠DPE on both sides: ∠EPA + ∠DPE = ∠DPB + ∠DPE i.e. ∠ = ∠
Consider the triangles ΔDAP and ΔEBP: ∠ DPA = ∠ (proven), ∠BAD = ∠ (given) and AP = (given)
By congruency rule, ΔDAP ≅ Δ
By CPCT: AD =
Hence, proved.

8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B as shown below. Prove that:

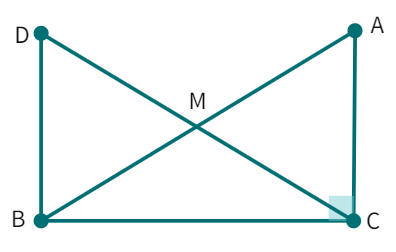
(i) ∆ AMC ≅ ∆ BMD

(ii) ∠ DBC is a right angle

(iii) ∆ DBC ≅ ∆ ACB

(iv) CM = 12 AB

Instructions

Prove the above statements

M is the mid-point of the line segment AB i.e. = BM. Also, ∠C = ° and DM = CM.
Considering the triangles ΔAMC and ΔBMD: AM = BM (given), CM = DM (given) and ∠CMA = ∠ ( angles)
By congruency criterion, ΔAMC ≅ Δ
By CPCT: ∠ACM = ∠ . Further more, they act as angles for the sides AC and BD.
Thus, AC || .
We can see that: ∠ ACB + ∠ DBC = ° (co-interiors angles). Thus, 90° + ∠B = 180° i.e. ∠B = ∠ DBC = °.
In the triangles ΔDBC and ΔACB: BC = CB (Common side), ∠ACB = ∠ ( angles) and DB = (Corresponding parts of proven Congruent Triangles)
By congruency rule: ΔDBC ≅ Δ.
By CPCT: DC =
We already have, DM = CM = AM = BM i.e. the point M is the mid-point for as well as .
Thus, DM + CM = BM + AM can be re-written as CM = i.e. CM = AB
Hence, proved.

Sign in to Innings2

Triangles

Reset Progress

Glossary

Exercise 7.1