Enhanced Curriculum Support
This is a comprehensive educational resource designed to provide students with the tools and guidance necessary to excel. This support system is structured to cater to various aspects of learning, ensuring that students are well-prepared for academic challenges and practical applications of mathematical concepts. Some are the key benefits are mentioned below:
Comprehensive Learning: This holistic approach helps students gain a thorough understanding of the subject. Practical Application: The resources encourage students to apply mathematical concepts to real-life scenarios, enhancing their practical understanding and problem-solving skills.
Critical Thinking and Reasoning: Value-Based and HOTS questions promote critical thinking and reasoning abilities. These skills are crucial for students to tackle complex problems and make informed decisions.
Exam Preparedness: Sample Question Papers and NCERT Exemplar Solutions provide ample practice for exams. They help students familiarize themselves with the exam format and types of questions, reducing exam anxiety.
Ethical and Moral Development: Value-Based Questions integrate ethical and moral lessons into the learning process, helping in the overall development of students' character and social responsibility. By incorporating these diverse elements, Enhanced Curriculum Support aims to provide a robust and well-rounded knowledge, preparing students for both academic success and real-world challenges.
Sec A
1. If the volume of a cube is 1728
(a) 144
2. A cube whose side is 5 cm will have surface area is equal to:
(a) 120
3. The dimensions of a rectangular iron box are l× w × h. How many times will the surface area of the iron box increase, if all its dimensions are doubled?
(a) 3 times (b) 5 times (c) 8 times (d) 4 time
4. If one side of a cube is 33 m, then the volume of the cube is:
(a) 35936
5. A metallic cylindrical pipe has outer radius of 3 cm and an inner radius of 2 cm. If the length of the pipe is 70 cm, then the volume of metal in the pipe, in
(a) 280 π (b) 630π (c) 910 π (d) 350 π
6. The sum of the radius of the base and the height of a cylinder is 37 m. If the total surface area of the solid cylinder is 1628
(a) 33 m (b) 44 m (c) 22 m (d) 11 m
7. The dimensions of an iron box are 9 ft × 4.4 ft × 2.5 ft. What is the cost of the iron sheet used to make the box, if the cost of the sheet is Rs 6 per square foot?
(a) Rs 887.2 (b) Rs 977.2 (c) Rs 777.2 (d) Rs 877.2
Sec B
1. A rectangular paper of width 14 cm is rolled along its width and a cylinder of radius 20 cm is formed. Find the volume of the cylinder. (Take π for
OR
A housing society consisting of 5500 people, needs 100 L of water per person per day. The cylindrical supply tank is 7 m high and has a diameter of 10 m. For how many days will the water in the tank last for the society?
Sec C
1. Rukhsar painted the outside of the cabinet of measure 1 cm × 2 cm × 1.5 cm. How much surface area did she cover if she painted all except the bottom of the cabinet.
2. An aquarium is in the form of a cuboid whose external measures are 80 cm × 30 cm × 40 cm. The base, side faces and back face are to be covered with a coloured paper. Find the area of the paper needed.
3. Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m. respectively. From each can of paint 100
Sec D
1. The length, width and height of a cuboid are 10cm, 8 cm and 7 cm respectively. Find the lateral surface area of a cuboid?
2. Find the area of the following fields. All dimensions are in metres.
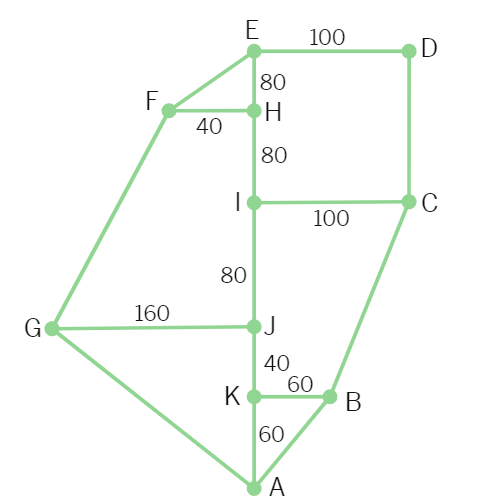
(OR)
The dimensions of a cuboid are in the ratio of 2 : 3 : 4 and its total surface area is 208
3. A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container. If the label is placed 2 cm from top and bottom, what is the area of the label.
4. In a building there are 24 cylindrical pillars each having a radius of 28cm and height of 4m. Find the cost of painting the curved surface area of all the pillars at the rate of Rs.8 per
OR
The dimensions of a cuboid are in the ratio of 2 : 3 : 4 and its total surface area is 208
Problem 1
A shopkeeper buys cylindrical containers to store rice. The radius of each container is 7 cm, and the height is 30 cm. Calculate the volume of each container. If the shopkeeper sells rice in these containers at a fair price, how does this practice benefit both the shopkeeper and the consumers? Reflect on the value of fairness in trade and how it leads to trust and better relationships in society.
Problem 2
The school decides to clean and paint the walls of its classroom, which are 4 m high, 6 m long, and 5 m wide. Calculate the total surface area of the walls to be painted. Why is maintaining cleanliness and hygiene important in schools? Discuss the value of keeping public spaces clean for everyone's benefit.
Problem 3
A sustainable housing project is using cuboidal bricks of size 20 cm by 10 cm by 5 cm. Calculate:
The surface area of each brick to determine the material needed for construction.
The volume of the brick to check how much space it will occupy.
Problem 4
A company is designing eco-friendly packaging in the shape of a cuboid for shipping goods. The dimensions of the box are 12 cm in length, 8 cm in width, and 5 cm in height. Calculate:
The surface area of the cuboid box to determine how much material is required for making the box.
The volume of the box to calculate the space available for packing items.
Q1
A school playground is being divided into three sections: a square-shaped garden, a cuboidal basketball court, and a circular fountain in the center. The square garden has a side length of 30 m, and the basketball court is a cuboid with a length of 20 m, a width of 10 m, and a height of 5 m.
If the total area available for the playground is 1500 m², and the fountain takes up 300 m², calculate the unused area.
Propose an alternative arrangement of the playground sections to utilize the available space efficiently. Discuss your reasoning with calculations.
Q2
A cylindrical can is to be designed to hold a certain volume of liquid, say 1000 cm³. You can vary the radius and height of the can but must maintain the same volume.
If the radius is doubled, how will the height change to maintain the same volume?
Which combination of radius and height would minimize the surface area, thereby minimizing the material required to make the can?
Q3
A shipping company has cuboidal boxes with dimensions 10 cm × 8 cm × 6 cm. The company receives an order for delivering items that require a box with at least 3000 cm³ of space. The company decides to combine several smaller boxes instead of designing a larger one.
How many of these smaller boxes are required to meet the volume requirement?
Is this approach more efficient in terms of surface area (material used) compared to using a single large box with the same volume? Justify your answer with calculations.
Choose the correct option
Questions
1. What is the area of the triangle ADE in the following figure?
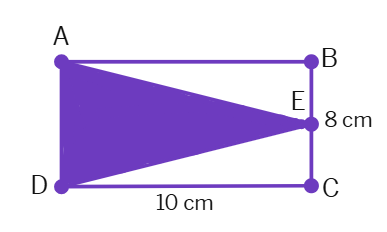
(a)45
2. What will be the change in the volume of a cube when its side becomes 10 times the original side?
(a) Volume becomes 1000 times.
(b) Volume becomes 10 times.
(c) Volume becomes 100 times.
(d) Volume becomes
160
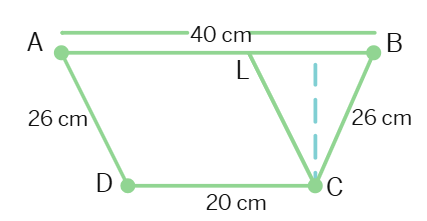
The parallel sides of a trapezium are 40 cm and 20 cm. If its non-parallel sides are both equal, each being 26 cm, find the area of the trapezium.
A cube of side 5 cm is painted on all its faces. If it is sliced into 1 cubic centimetre cubes, how many 1 cubic centimetre cubes will have exactly one of their faces painted?
(a) 27 (b) 42 (c) 54 (d) 142
A circle of maximum possible size is cut from a square sheet of board. Subsequently, a square of maximum possible size is cut from the resultant circle. What will be the area of the final square?
(a)
(c)
What is the area of the largest triangle that can be fitted into a rectangle of length l units and width w units?
(a)
The surface area of the three coterminus faces of a cuboid are 6, 15 and 10
(a) 30
A regular hexagon is inscribed in a circle of radius r. The perimeter of the regular hexagon is:
(a) 3r (b) 6r (c) 9r (d) 12r
The volume of a cylinder whose radius r is equal to its height is:
(a)
What is the area of the rhombus ABCD below if AC = 6 cm, and BE = 4cm?
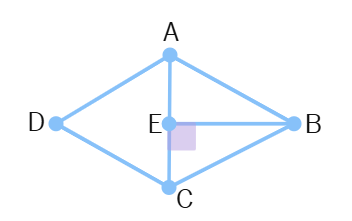
(a) 36
A covered wooden box has the inner measures as 115 cm, 75 cm and 35 cm and thickness of wood as 2.5 cm. The volume of the wood is:
(a) 85,000
Ramesh has three containers.
(a) Cylindrical container A having radius r and height h,
(b) Cylindrical container B having radius 2r and height
(c) Cuboidal container C having dimensions r × r × h
The arrangement of the containers in the increasing order of their volumes is:
(a) A, B, C
(b) B, C, A
(c) C, A, B
(d) cannot be arranged
If R is the radius of the base of the hat, then the total outer surface area of the hat is:
(a) πr (2h + R) (b) 2πr (h + R)
(c) 2 πrh +
Fill in the blanks
Questions
The surface area of a cuboid formed by joining two cubes of side a face to face is ?
A cube of side 5 cm is cut into 1 cm cubes. The percentage increase in volume after such cutting is ?
If the diagonals of a rhombus get doubled, then the area of the rhombus becomes ? its original area.
If the diagonal d of a quadrilateral is doubled and the heights h1 and h2 falling on d are halved, then the area of quadrilateral is ?
Opposite faces of a cuboid are ? in area.
Two cylinders A and B are formed by folding a rectangular sheet of dimensions 20 cm × 10 cm along its length and also along its breadth respectively. Then volume of A is ? of volume of B.
State True or False
Questions
Ratio of area of a circle to the area of a square whose side equals radius of circle is 1 : π.
1L = 1000
Amount of region occupied by a solid is called its surface area.
Two cuboids with equal volumes will always have equal surface areas.
A cube of side 3 cm painted on all its faces, when sliced into 1 cubic centimetre cubes, will have exactly 1 cube with none of its faces painted.
The area of a trapezium become 4 times if its height gets doubled.
Answer the following questions
Questions
Four horses are tethered with equal ropes at 4 corners of a square field of side 70 metres so that they just can reach one another. Find the area left ungrazed by the horses.
A cube of side 5 cm is cut into as many 1 cm cubes as possible. What is the ratio of the surface area of the original cube to that of the sum of the surface areas of the smaller cubes?
A wooden box (including the lid) has external dimensions 40 cm by 34 cm by 30 cm. If the wood is 1 cm thick, how many
A river 2 m deep and 45 m wide is flowing at the rate of 3 km per hour. Find the amount of water in cubic metres that runs into the sea per minute.
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?

External dimensions of a closed wooden box are in the ratio 5![]() 3. If the cost of painting its outer surface at the rate of Rs 5 per
3. If the cost of painting its outer surface at the rate of Rs 5 per
A cylindrical tank has a radius of 154 cm. It is filled with water to a height of 3 m. If water to a height of 4.5 m is poured into it, what will be the increase in the volume of water in kl?
How many bricks of size 22 cm × 10 cm × 7 cm are required to construct a wall 11m long, 3.5 m high and 40 cm thick, if the cement and sand used in the construction occupy
Q1
While constructing his house, Karan has constructed an underground water tank and an overhead water tank. The underground tank is also called a sump to which the municipal water pipe is connected.
In the city where Karan lives, the local municipal water is supplied every alternate day. The sump in Karan’s house is in the shape of a cuboid with the following dimensions: length = 2 m; breadth = 1.5 m and height = 2 m. The cylindrical overhead tank kept on the terrace needs to be filled by pumping water from the sump, every day. The radius of the overhead tank is 0.7 m and its height is 2 m.
1. What is the volume of water left in the sump after filling the overhead tank with water from the sump? Assume that initially the sump was full and the overhead tank was empty. (Note: 1 cubic metre = 1000 litres).
2. (i) To address frequent water scarcity problems, Karan wanted to increase the water storage capacity by another 1000 litres. Constructing another sump would have required modifications to his house design. Hence he decided to build another overhead tank instead. The new tank is in the shape of a cube which can hold 1000 litres of water. What would be the side of this cube-shaped tank?
(ii) If the lengths of all three sides of the cube-shaped tank are reduced by half, what would be the quantity of water that could be filled in the new tank?
(a) 750 litres (b) 500 litres
(c) 250 litres (d) 125 litres
Sol 1
Solution:
1. Volume of Water Left in the Sump:
Sump dimensions: Length = 2 m, Breadth = 1.5 m, Height = 2 m
- Volume of sump = 2 × 1.5 × 2 = 6, cubic meters
Overhead tank dimensions: Radius = 0.7 m, Height = 2 m
Volume of overhead tank = pi ×
0.7 2 Volume in liters = 3.078 × 1000 = 3078 liters
Initial volume of water in sump = 6000 liters.
Remaining water in the sump = 6000 - 3078 = 2922 liters.
2. Cube-Shaped Tank:
The new cube-shaped tank can hold 1000 liters (1 cubic meter).
Side length of the cube = 1 meter.
3. New Cube Dimensions (when side lengths are halved):
New side length =
1 2 Volume of new cube =
0.5 3
Thus, the new smaller cube-shaped tank can hold 125 liters of water.
Q2
Waterproofing of the sump/tank is done in order to avoid leakage of water. Usually it is done by applying a layer made of a mixture of cement and polymer to the bottom surface and all the side walls of a sump/tank, from the inside. To avoid any leakage in the future, Karan wanted to get the sump waterproofed. The contractor quoted a price of ₹500 per
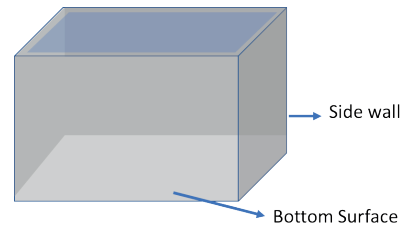
1. What is the total area of the part of the sump to be waterproofed? (refer to Case Study B, Sump & Overhead Tank, above, for the dimensions of the sump)
2. In Karan’s opinion, for long-term use, both of his overhead tanks will also have to be water proofed in order to avoid leakages in the future. As the quotation from the contractor says there will be a reduction in the price if the total area is more than 25
(i) What is the total area of cylindrical and cube-shaped tanks to be waterproofed? (refer to Case Study B, Sump & Overhead Tank, above, for the dimensions of the cylindrical tank and Question 5 (i) for the dimensions of the cube-shaped tank)
(ii) How much extra does he have to pay if he does waterproofing for the sump and the two overhead tanks instead of just doing it for the sump?
Sol 2
Solution:
1. Total Area of the Sump to be Waterproofed:
The sump is a cuboid with dimensions: Length = 2 m, Breadth = 1.5 m, Height = 2 m.
The area to be waterproofed includes the bottom and all side walls.
Total area to be waterproofed = 17 m².
2. Total Area of the Cylindrical and Cube-Shaped Tanks to be Waterproofed:
Cylindrical Tank (radius = 0.7 m, height = 2 m): Total area = 11.874 m².
Cube-Shaped Tank (side = 1 m): Total area = 6 m².
Total area of both tanks = 17.874 m².
3. Extra Amount to be Paid for Waterproofing the Sump and Two Tanks:
Total area for sump and two tanks = 34.874 m².
Since the total area is more than 25 m², the cost is ₹400 per m².
Cost for sump only = ₹7550 (including labor).
Cost for sump and both tanks = ₹14699.6 (including labor).
Extra amount to be paid = ₹7149.6.
Thus, Karan would pay an additional ₹7149.6 if he decides to waterproof the sump and both overhead tanks instead of just the sump.
Q3
The keel is one of the most important parts of a sailboat. It is a flat blade sticking down into the water from a sailboat's bottom. Without the keel, strong side-winds would simply push the boat sideways or flip it over. The keel will offer resistance (an opposing force) to such sideways motions caused by the wind and keep the boat stable. The stability offered by the keel depends on the area of the keel. Less area means less stability. Usually a keel is shaped like a trapezium, with its top and bottom being parallel to each other. Another major factor that affects the resistance offered by the keel is the height of the keel. Larger keel height will result in larger resistance.

Sailboat and keel and schematic of wind direction and keel resistance; Image by Paul Schultz and Fibonacci (talk) via Wikimedia Commons
1. The figure shows the schematic of a sailboat with a keel attached at the bottom. Calculate the area of the keel.
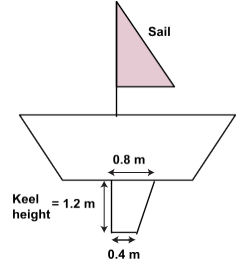
Keel measurements in a sailboat (figure not to scale)
2. The figure shows two sailboats, A and B, of the same size. But the dimensions of their keel are different. Purely based on the area of the keel, which sailboat will remain more stable against the wind if both are travelling under the same conditions?
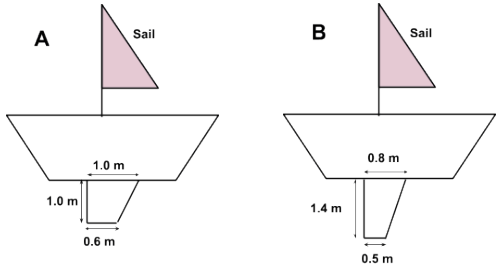
Two sailboats with different keel dimensions (figure not to scale)
3. The figure shows four different ship types and the table gives the length of each ship type and corresponding keel height. By looking at these values we can infer that longer ships will have more keel height.

Ship types: 1. Steamboat; Image by Murgatroyd49; 2. Barge; Image by Vmenkov; 3. Mega yacht; Image by Noah Wulf; 4. Sports boat; Image by Bengt Nyman Via Wikimedia Commons
| Ship Type | Ship Length | Keel Height |
|---|---|---|
| Steamboat | 122 m | 5.50 m |
| Barge | 110 m | 4.85 m |
| Mega yacht | 69 m | 3.35 m |
| Sport boat | 8 m | Less than 2 m |
onsider a ship with a trapezium-shaped keel. The lengths of the parallel sides are in a ratio 2 : 5, and the length of the smaller of the parallel sides is 0.6 m. The area of the keel is 3.5
Sol 3
Solution:
1. Calculate the Area of the Keel:
- The keel is typically shaped like a trapezium, with the area calculated using the formula:
Area of trapezium =
where
2. Sailboat Stability:
The stability of a sailboat is directly related to the area of its keel. A larger keel area offers more resistance to side winds, making the boat more stable.
Between two sailboats, the one with the larger keel area will remain more stable under the same conditions. Therefore, you compare the areas of their keels to determine which boat will be more stable.
3. Ship Type and Keel Dimensions:
The ship's keel area and height are related to the ship's size. A larger ship generally requires a larger keel for more resistance against the wind.
For a trapezium-shaped keel with parallel sides in a 2:5 ratio, and the smaller parallel side being 0.6 m with an area of 3.5 m², you can calculate the other dimensions of the keel and infer which ship type the keel likely belongs to based on its keel height and area.
Calculation:
Let
b 1 b 2 5 2 Using the area formula for a trapezium and substituting the known values:
3.5 =
3.5 =
h =
The calculated height of the keel is approximately 3.33 meters, which is closest to the Mega yacht keel height (3.35 m).
The trapezium-shaped keel with the given dimensions and area would most likely belong to the Mega yacht, as its keel height matches closely with the calculated height.
