Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 9: Mensuration

    Introduction

    Area of a Polygon

    Solid Shapes

    Surface Area of Cube, Cuboid and Cylinder

    Volume of Cube, Cuboid and Cylinder

    Volume and Capacity

    Exercise 9.1

    Exercise 9.2

    Exercise 9.3

    What Have We Discussed?

    Enhanced Curriculum Support

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 9: Mensuration > Exercise 9.1

Exercise 9.1

1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.

Instructions

One parallel side of the trapezium (a) = 1 m while the other side (b) = m with height (h) = m
Area of top surface of the table = × ×
Area of top surface of the table = = 12 × (1+1.2)0.8 = 12 × × 0.8 =
Area of top surface of the table is 0.88 m2.

2. The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.

Instructions

Let the length of the other parallel side be b.
We have: Length of one parallel side (a) = cm with height (h) = cm and area of a trapezium = cm2
Area of trapezium = 12×a+bh i.e. 34 = 12(10+b)×4 giving us: 34 = 2×10+b
So, b = cm.
Hence, another required parallel side is 7 cm.

3. Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Area of the field

Instructions

Finding length of AB

  • Using the given data: Length of AB = m.
  • Area of trapezium: where h - height , a and b - the length of the parallel sides.
  • Substituting the value we get
  • Total area of field: m2
  • We got the respective results.

4. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.

Instructions

Let h1 = 13 m, h2 = 8 m and AC = 24 m
Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ADC = 12(bh1)+ 12(bh2) = 12 × bh1+h2 = 12××(13+8) = 12×× = m2
Hence, the required area of the field is 252 m2.

5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.

Instructions

Area of rhombus ?

  • We know that, Area of rhombus: where p and q - lengths of the two diagonals.
  • Substituting the value we get
  • Area of rhombus: cm2
  • We have got the respective result.

6. Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.

Instructions

Area of rhombus ?

  • We know that a rhombus is a type of .
  • We also know, Area of parallelogram: where b - base length and h - height
  • Area of rhombus: cm2
  • Area of rhombus: where p and q - lengths of the two diagonals.
  • Substituting the obtained values.
  • Length of second diagonal: cm
  • We have got the respective result.

7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is Rs 4.

Instructions

Finding area of each tile

  • We know, Area of rhombus: where p and q - lengths of the two diagonals.
  • Substituting the value we get
  • Area of each tile: cm2
  • Area of floor: m2
  • Thus, cost of polishing the floor: Rs.
  • We got the desired result.

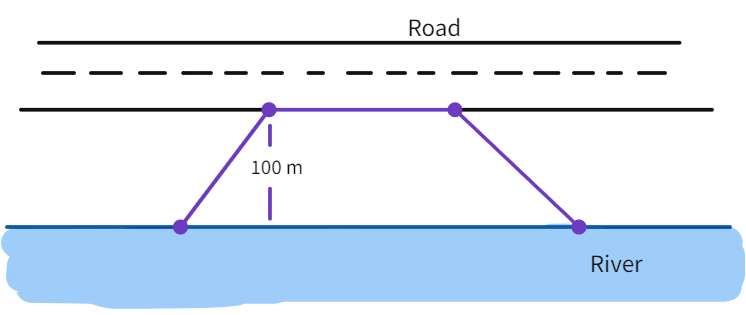
8. Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.

Area of field

Instructions

Assume 'x' as field length along the road

  • Thus, length along river will be .
  • Area of trapezium field: where h - height , a and b - the length of the parallel sides.
  • Substituting the value we get
  • Value of x: m
  • Thus, length along river: m
  • We have got the desired result.

9. Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

Instructions

The octagon has equal sides: each m.
Divide the octagon as shown in the below figure, two (s) whose parallel and perpendicular sides are m and m respectively and third one is having length and breadth m and m respectively.
Area of two trapeziums = 2 × 12 × a+b×h = 2 × 12 × (11+5) × 4 = 4 × = m2.
Area of rectangle = length × breadth = × =
Thus, Total area of octagon = 64 + 55 = m2

10. There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways. Find the area of this park using both ways. Can you suggest some other way of finding its area?

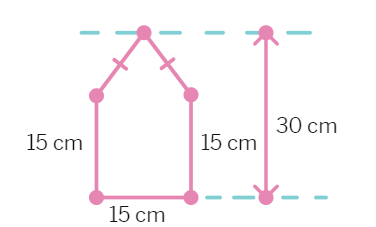
Jyoti's Diagram

Instructions

Using Jyoti’s diagram:

Area of pentagon = Area of trapezium ABCP + Area of trapezium AEDP = 12(AP+BC) × CP + 12 × (ED+AP)× DP = 12(+) × CP + 12 × (+)× DP
= 12×(30+15)×(CP+DP) = 12××
= 12 × 45 × = m2
Area of pentagon is 337.5 m2

Kavita's diagram

Using Kavita’s diagram

We have: a perpendicular AM drawn to BE. So, AM = – = m
We see: Area of pentagon = Area of triangle ABE + Area of square BCDE
Area of pentagon = 12 × × + (×) = + = m2
Area of pentagon is 337.5 m2

11. Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.

Dimensions of frame

Instructions

Finding area of each frame

  • We observe that the two frames along the length are identical to each other. The same is true for the frames along the breadth.
  • Using the given dimensions, the width of the frame: cm.
  • Area of each frame: where h - height , p and q - the length of the parallel sides.
  • Substituting the value we get
  • Area of frame along length: cm2
  • Area of frame along breadth: cm2
  • We got the desired result.