Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 9: Mensuration

    Introduction

    Area of a Polygon

    Solid Shapes

    Surface Area of Cube, Cuboid and Cylinder

    Volume of Cube, Cuboid and Cylinder

    Volume and Capacity

    Exercise 9.1

    Exercise 9.2

    Exercise 9.3

    What Have We Discussed?

    Enhanced Curriculum Support

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 9: Mensuration > Volume of Cube, Cuboid and Cylinder

Volume of Cube, Cuboid and Cylinder

We have spoken about surface area but another very important related quantity when it comes to solids and shapes is Volume. The amount of space occupied by a three dimensional object is called its volume. For example: The space is a room is greater than the space in a cabinet. In other words, the volume of the room is greater than the volume of the cabinet. Similarly, the volume of a pencil box will be greater than the volume of the pen and the eraser kept inside it.

In terms of real life applications, how many bottles of water can we place in a small store room? What is the amount of milk that can be carried by the milkman if he has two containers with a fixed value of dimensions? Such problems can only be solved when we check for the related volumes.

Now, how to measure the volume of any of these objects?

We use square units- m2,cm2 etc. for denoting the area of a region. Now, we will be using cubic units to find the volume of a solid, as a cube is the most convenient solid shape (just as square is the most convenient shape to measure area of a region). Just like for finding the area, we divide the region into square units, similarly, to find the volume of a solid we need to divide it into cubical units.

Division of Volume

The volume of a solid can be said to be measured by counting the number of unit cubes it contains. Cubic units which we generally use to measure volume is equal to:

1 cubic cm = 1 cm × 1 cm × 1 cm = 1 cm3 = 10 mm × 10 mm × 10 mm = 1000 mm3

1 cubic m = 1 m × 1 m × 1 m = 1 m3 = 106cm3

1 cubic mm = 1 mm × 1 mm × 1 mm = 1 mm3 = 0.1 cm × 0.1 cm × 0.1 cm = ...................... cm3

Let's start by finding the volume formula for the basic shapes of cube, cuboid and cylinder.

Cuboid

In the below table, consider the sides and assign them the designation of "length" , "breadth" and "height". Now, take the numerical values and find the product of length×breadth×height. (Each cube has a dimension of 1 x 1 x 1 unit)

S.NoCuboidl×b×h
(i) unit3
(ii) unit3
(iii) unit3

We observe that the numerical value of the product l×b×h is the same as the number of unit cubes present in the respective arrangement. This product is the volume of the cuboid.

Since, l×b is also the area of the face taken to be the base of the cuboid, we can also write:

Volume of cuboid = Area of base × height

Volume of cuboid = area of the base × height = l x b x h

Take 36 cubes of equal size (i.e., length of each cube is same). Arrange them to form a cuboid. What do you observe? Since we have used 36 cubes to form these cuboids, volume of each cuboid is 36 cubic units. Also volume of each cuboid is equal to the product of length, and of the cuboid.

Try These

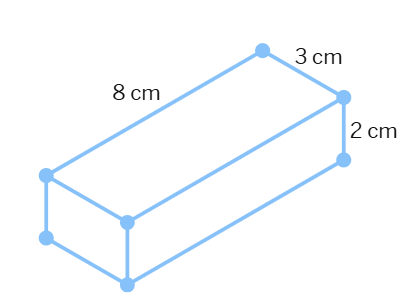
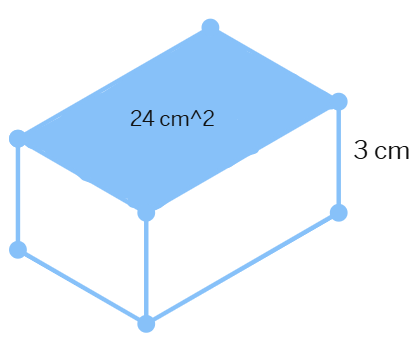
Find the volume of the following cuboids.

Instructions

(i) Let l = 8 cm, b = 3 cm and h = cm
We have the volume as
Thus, Volume = cm3.
(ii) We have area of base = cm2 and h = cm
We have: volume as
Thus, Volume = cm3.

Cube

We have already spoken about how, the cube is a special case of a cuboid where l = b = h. By simply putting this condition into the above equation for volume of cuboid:

Instructions

Putting the same value for l,b and h

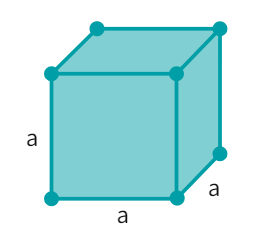
  • Let l = b = h = a. Thus, volume of cuboid with all sides equal i.e. a cube: unit3
  • Thus, volume of cube becomes as shown.

Thus,

Volume of cube = a3

where, a is the cube side length.

TRY THESE

Find the volume of the following cubes: (a) with a side 4 cm (b) with a side 1.5 m

Instructions

Volume =
(a) For a cube with side 4 cm: Volume = 43 = cm3
(b) For a cube with side 1.5 m: Volume = 1.53 = m3

Arrange 64 cubes of equal size in as many ways as you can to form a cuboid. Find the surface area of each arrangement. Can solid shapes of same volume have same surface area?

Instructions

For a cuboid with dimensions a × b × c, the surface area formula is: Surface Area = (ab + bc + ac)
Let's find all possible arrangements of 64 cubes: 1 × 1 ×
Surface Area = 2(1×1 + 1×64 + 1×64) = 2( + + ) = 2() = square units
1 × 2 × 32: Surface Area = 2(1×2 + 2×32 + 1×32) = 2( + + ) = 2() = square units
1 × 4 × 16: Surface Area = 2(1×4 + 4×16 + 1×16) = 2( + + ) = 2() = square units
1 × 8 × 8: Surface Area = 2(1×8 + 8×8 + 1×8) = 2( + + ) = 2() = square units
2 × 2 × 16: Surface Area = 2(2×2 + 2×16 + 2×16) = 2( + + ) = 2() = square units
2 × 4 × 8: Surface Area = 2(2×4 + 4×8 + 2×8) = 2( + + ) = 2() = square units
2 × 8 × 4: Surface Area = 2(2×8 + 8×4 + 2×4) = 2( + + ) = 2() = square units
4 × 4 × 4: Surface Area = 2(4×4 + 4×4 + 4×4) = 2( + + ) = 2() = square units
, solid shapes with the same volume can have the same surface area.
In our example, we can see that arrangements: 2×4×8 and 2×8×4 have the same surface area (112 square units) while having the same volume (64 cubic units).
However, it's important to note that among all possible cuboids with a given volume, the cube arrangement 4×4×4 always has the surface area.

Cylinder

When it comes to the volume of the cylinder - similar to cuboid, a cylinder has got a top and a base which are congruent and parallel to each other and its lateral surface is perpendicular to the base.

We also know that the volume of a cuboid can be found by finding the product of area of base and its height. Using that same logic to cylinders, we get:

Instructions

Calculating volume of a cylinder

  • Volume of a cylinder: (circular base) x (height)
  • Thus, if cylinder radius and height are r and h respectively, the volume of a cylinder: unit3
  • Thus, volume of a cylinder becomes as shown.

Thus,

Volume of cylinder = area of base × height = πr2 x h = πr2h

A company sells biscuits. For packing purpose they are using cuboidal boxes:

(1) Box A = 3 cm × 8 cm × 20 cm

(2) Box B = 4 cm × 12 cm × 10 cm

What size of the box will be economical for the company?

Instructions

Which is more economical ?

  • First, let's calculate the volume of both the boxes.
  • Volume(Box A) = cm3 while Volume(Box B) = cm3
  • We see that both are equal.
  • In order to check which box is more economical, we can check the material used for packaging i.e. we need to calculate the of the boxes. Also
  • Surface area of a box of length l, breadth b and height h =
  • Thus, Surface area for A = Material needed for box A = cm2
  • Surface area for B = Material needed for box B = cm2
  • Thus, is more economical as it will be using lesser amount of material.
  • Thus, Box B is more economical for the manufacturers.

Find the volume of the following cylinders.

(i) r = 7 cm and h = 10 cm

(ii) base area = 250 m2 and h = 2 m

Instructions

Volume =
(i) For a cylinder with r = 7 cm and h = 10 cm: Volume = π × 72 × 10 = × × 10 = cm3
(ii) For a cylinder with base area = 250m2 and h = 2 m: Since the base area = πr2, we can directly use: Volume = base area × = m2 × m = m3
We have found the answers.