Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 9: Mensuration

    Introduction

    Area of a Polygon

    Solid Shapes

    Surface Area of Cube, Cuboid and Cylinder

    Volume of Cube, Cuboid and Cylinder

    Volume and Capacity

    Exercise 9.1

    Exercise 9.2

    Exercise 9.3

    What Have We Discussed?

    Enhanced Curriculum Support

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 9: Mensuration > Surface Area of Cube, Cuboid and Cylinder

Surface Area of Cube, Cuboid and Cylinder

Say, we have a cuboidal, cubical and a cylindrical box- all having the same height. If these boxes need to be painted, can you deduce which box requires more amount of paint? Logically, we know that the box with the most amount of surface area will be using up more paint? But which box has the highest value of surface area?

To find the total surface area of any object, we need to find the area of each face of that object and add up all the values. Thus,

The surface area of a solid is the sum of the areas of its faces.

The cylinder has congruent circular faces that are parallel to each other (Fig 9.12). Observe that the line segment joining the center of circular faces is perpendicular to the base. Such cylinders are known as right circular cylinders. We are only going to study this type of cylinders, though there are other types of cylinders as well (Fig 9.13).

Why is it incorrect to call the solid shown here a cylinder?

Cuboid

A cuboid is a 3D object, having the length, breadth and height as dimensions (the values for atleast two dimensions is unequal) and the opposite faces are identical.

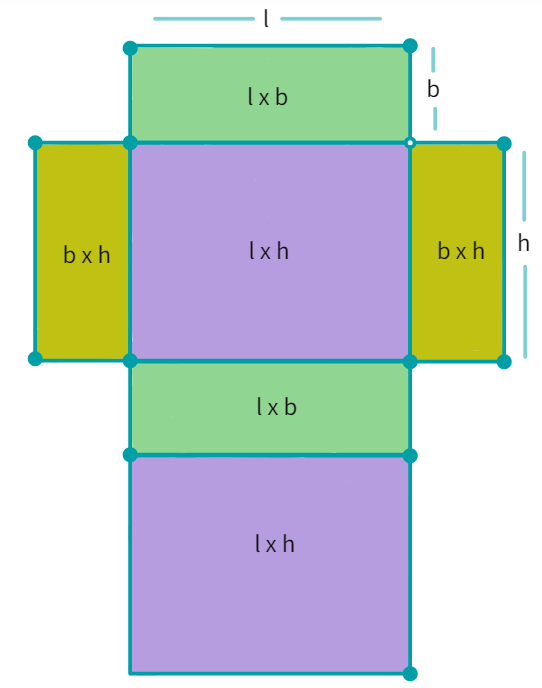
Since, a cuboid has a total of six faces- it has pairs of identical faces.

To find the total surface area:

The Total surface area of a cuboid = h × l + b × l + b × h + l × h + b × h + l × b

= 2(lb + bh + hl)

Total surface area = 2 (h × l + b × h + b × l) = 2(lb + bh + hl)

where h, l and b are the height, length and width of the cuboid respectively.

When we consider, the surface of a room to be painted, how much paint will be needed? We realize that the roof and floor need not be included for this calculation. Like this, there are many cases where only the sides (excluding the top and base) of the solid need to be taken into account. In such cases, we calculate the lateral surface area.

In the case regarding the room, we calculate the lateral surface area of the cuboid.

Lateral surface area of a cuboid = 2(h × l + b × h) (or) 2h (l + b)

Can we say that:

Total surface area of cuboid = lateral surface area + 2 × area of base? (Yes/No)

We have a cuboid with length (l), breadth(b) and height (h), where the numerical values for all the dimensions are different.If we interchange the length and the height of the cuboid to obtain a new cuboid, will its lateral surface area change? (Yes/No)

The new lateral surface area will be equal to:

Given: length = 15 cm , breadth = 10 cm and height = 20cm, find the value of the surface area of the cuboid.

Instructions

Total surface area=2l×b+b×h+h×l

  • Substituting the values, we get: Surface Area = cm2
  • Substituting the values
  • Adding
  • We have found the result.

TRY THESE

Find the total surface area of the following cuboids:

Instructions

Total Surface Area =
For the cuboid with dimensions 6 × 4 × 2 cm: Total Surface Area = 2(6×4 + 4×2 + 6×2) = 2( + + ) = 2() = cm2
For the cuboid with dimensions 4 × 4 × 10 cm: Total Surface Area = 2(4×4 + 4×10 + 4×10) = 2( + + ) = 2() = cm2

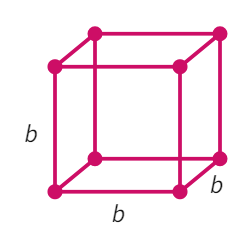
Cube

In the case of cuboid, the length, breadth and height is assumed to be of unequal numerical values. But if

length(l) = breadth(b) = height (h) for a cuboid

We get a cube. Just like a cuboid, a cube also has a total number of 6 faces but each face is a square, instead of a rectangle. We already know that the area of a square with side length 'a' is:

Thus,

Total surface area of cube =

The total surface area of a cube = 6a2 where, a is the length of a side.

Find the surface area of cube A and lateral surface area of cube B.

Instructions

For cube A with side length 10 cm: Total surface area = × side2 = 6 × = 6 × = cm2
For cube B: the lateral surface area is 8 cm. We know that lateral surface area of a cube = × side2
So 4 × side2 = 8 cm which gives us: side2 = ÷ = cm. Thus, side = cm
Total surface area = 6 × side2 = 6 × = cm2

How will you arrange 12 cubes of equal length to form a cuboid of smallest surface area?

Instructions

Think about all the possible arrangements

  • The possible arrangements include:
  • 12×1×1, 2×3×2 and 6×2×1
  • Calculating the surface area for each:
  • For: 12×1×1 = cm2, 2×3×2 = cm2, 6×2×1 = cm2
  • Thus, we have found the arrangement with the smallest surface area i.e.

Solution: Let's start with the easiest problem and build up from there logically. It is obvious that the cubes having 3 faces painted will be the ones situated at the corners of the bigger cube. Given, there are 8 corners in a cube:

The number of cubes with 3 painted faces = 8

We know that:

Volume of cube = a3 = 64 cubes

64 = a3

a = 4 units i.e. 4 cubes were made along each edge.

Moving on, cubes aligned along the edges would have two painted faces. Since, 2 cubes are along each edge (excluding the corner cubes):

The number of cubes with 2 painted faces = 2 × number of edges = 2 × 12 = 24

Moving on to cubes with 1 face painted, they will be the cubes which were on the face surface but not at the edges (or) corner.

Each face had 4×4 = 16 cubes.

Remaining cubes after removing corner/edge cubes = 16 - 12 = 4

Thus, each face has 4 cubes with one painted face. The total number of faces of a cube is equal to 6.

Number of cubes having 1 face painted = 4 × 6 = 24

Remaining cubes out of 64 will have no face painted = 64 - 24 - 24 - 8 = 8

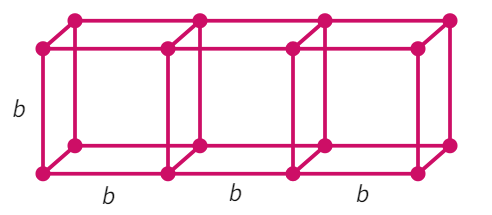
Two cubes each with side b are joined to form a cuboid.

Instructions

Finding surface area of two cubes together

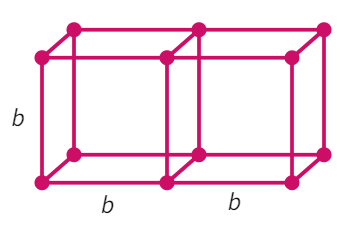
  • When two cubes are together: l = , b = and h =
  • Thus, surface area of this cuboid:
  • When three cubes are put together: l = , b = and h =
  • Thus, surface area of the second cuboid:
  • We have found the desired answers.

Cylinders

Most of the real life examples of a cylinder we see day to day are right circular cylinders. For example: a can, cylinderical pillars, tube lights, pipes etc. When we try to draw a net for such cylinders, we get:

1. Top and base faces are circles of radius "r"

2. The curved(lateral) surface, upon being cut along the vertical length, giving a rectangle of length "2πr" and breadth of "h"

Flower Can

Cold drink can

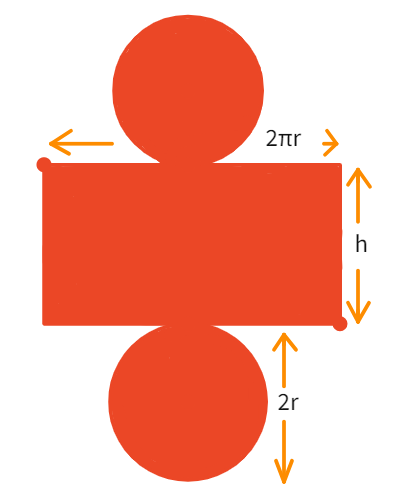
Cylinder Net

Instructions

Observe the above given figure

  • We can see that: Surface Area of Cylinder = × Top/Base Circle + Lateral surface
  • Thus, Surface Area of Cylinder = 2 × + where r and h are radius and height of the cylinder.
  • Simplifying, we get: Surface Area of Cylinder = 2πr(r + h)
  • We have found the surface area formula for a cylinder.

If we need just the lateral surface area(excludes top and base circle):

Lateral surface Area of Cylinder = 2πrh

The lateral (or curved) surface area of a cylinder = 2πrh

The total surface area of a cylinder = πr2 + 2πrh + πr2 = 2πr (r + h)

We have seen that lateral surface area of a cylinder is the circumference of base × height of cylinder. Can we write lateral surface area of a cuboid as perimeter of base × height of cuboid?

Instructions

Similar to the case with cylinder

  • Using the same method used for cylinder we can say: The lateral surface area of a cuboid = 2h (l + b) (A) . But is it true? Let's verify.
  • We know that: perimeter of the base of a cuboid = 2(l + b) (B)
  • Upon multiplying the height to the perimeter, we get: 2h (l + b)
  • Comparing equations (A) and (B) we can see that the above mentioned statement is true.

Lateral surface area (cuboid) = Base Perimeter × h

In general,

The formulae of Lateral Surface Area for cube, cuboid and cylinder is base perimeter multiplied into height.

Find total surface area of the following cylinders:

(i) r = 14 cm, h = 8 cm

(ii) d = 2 m , h = 2 m

Instructions

Total Surface Area =
(i) For a cylinder with r = 14 cm and h = 8 cm: Total Surface Area = 2π × × ( + ) = 2π × × = π cm2 = cm2 (Round off to two decimal places)
(ii) For a cylinder with d = 2 m and h = 2 m: Find the radius: r = d2 = m
Total Surface Area = = 2π × × (1 + 2) m2 = 2π × × = 2π × = π = m2 (Round off to two decimal places)

Example 4: An aquarium is in the form of a cuboid whose external measures are 80 cm × 30 cm × 40 cm. The base, side faces and back face are to be covered with a coloured paper. Find the area of the paper needed?

Instructions

We have: The length of the aquarium = l = cm and Width of the aquarium = b = cm while Height of the aquarium = h = cm
Area of the base = l × b = × = cm2
Area of the side face = b × h = × = cm2
Area of the back face = l × h = × = cm2
Required area = Area of the base + area of the back face
  • ( × area of a side face) = + + ( × ) = cm2
Hence the area of the coloured paper required is 8000 cm2.

Example 5: The internal measures of a cuboidal room are 12 m × 8 m × 4 m. Find the total cost of whitewashing all four walls of a room, if the cost of white washing is Rs. 5 per m2. What will be the cost of white washing if the ceiling of the room is also whitewashed.

Instructions

Let the length of the room = l = m, Width of the room = b = m and Height of the room = h = m
Area of the four walls of the room = of the base × of the room
Thus, Area of the four walls of the room = (l + b) × h = ( + ) × = × × = m2
Cost of white washing per m2 = Rs. 5. Hence the total cost of white washing four walls of the room = Rs. (160 × 5) = Rs.
Area of ceiling is 12 × 8 = m2
Cost of white washing the ceiling = Rs. (96 × 5) = Rs.
So, the total cost of white washing = Rs. (800 + 480) = Rs.

Example 6: In a building there are 24 cylindrical pillars. The radius of each pillar is 28 cm and height is 4 m. Find the total cost of painting the curved surface area of all pillars at the rate of Rs. 8 per m2.

Instructions

Radius of cylindrical pillar, r = 28 cm = m and height, h = 4 m
Curved surface area of a cylinder =
Curved surface area of a pillar = 2 × × × = m2
curved surface area of 24 such pillar = 7.04 × = m2
Cost of painting an area of 1 m2 = Rs. 8 Therefore, cost of painting 1689.6 m2 = × 8 = Rs.

Example 7:Find the height of a cylinder whose radius is 7 cm and the total surface area is 968 cm2.

Instructions

Finding height of cylinder

  • We know that, total surface area of cylinder of radius(r) and height(h): unit2
  • Substituting the values we get
  • The value of h (height): cm
  • The value has been found.

Find the surface area and the lateral surface area of a cube of side equal to 5 units.

Instructions

Putting the value in the respective equations

  • We know that, total surface area of cube: unit2
  • And the lateral surface area of cube: unit2
  • Substituting the value we get
  • Total surface area of cube: unit2
  • Lateral surface area of cube: unit2
  • We got the respective results.

If the cube in the previous question is elongated to a height of 10 units, it becomes a and the new surface area and the lateral surface area are:

Instructions

The new length is 10 units

  • We know that, total surface area of cuboid of length(l), breadth(b) and height(h): unit2
  • And the lateral surface area of cuboid: unit2
  • Substituting the values we get
  • Total surface area of cuboid: unit2
  • Lateral surface area of cuboid: unit2
  • We have found the respective results.

A cube has a side length of 7 cm while a cylinder has a diameter and height of 7cm. Which solid has the higher lateral surface area?

Instructions

Solid with larger lateral surface area

  • Lateral area of cube: where a - side length
  • Lateral area of cylinder: where r - radius and h - height
  • Substituting the values we get:Lateral area of cube: cm2
  • Lateral area of cylinder: cm2
  • Thus, the solid with the larger lateral area is: