Angle Subtended by an Arc of a Circle
You have seen that the end points of a chord other than diameter of a circle cuts it into two arcs – one major and other minor.
If you take two equal chords, what can you say about the size of arcs? Is one arc made by first chord equal to the corresponding arc made by another chord? In fact, they are more than just equal in length. They are congruent in the sense that if one arc is put on the other, without bending or twisting, one superimposes the other completely.
You can verify this fact by cutting the arc, corresponding to the chord CD from the circle along CD and put it on the corresponding arc made by equal chord AB. You will find that the arc CD superimpose the arc AB completely. This shows that equal chords make congruent arcs and conversely congruent arcs make equal chords of a circle. You can state it as follows:
If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal.
Also the angle subtended by an arc at the centre is defined to be angle subtended by the corresponding chord at the centre in the sense that the minor arc subtends the angle and the major arc subtends the reflex angle.
Therefore, in the figure, the angle subtended by the minor arc PQ at O is ∠POQ and the angle subtended by the major arc PQ at O is reflex angle POQ.
In view of the property above and the theorem stating that equal chords of a circle subtend equal angles at the centre, the following result is true:
Congruent arcs (or equal arcs) of a circle subtend equal angles at the centre.
Therefore, the angle subtended by a chord of a circle at its centre is equal to the angle subtended by the corresponding (minor) arc at the centre. The following theorem gives the relationship between the angles subtended by an arc at the centre and at a point on the circle.
Theorem 9.7
Central Angle and Inscribed Angle Theorem: The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Proof:
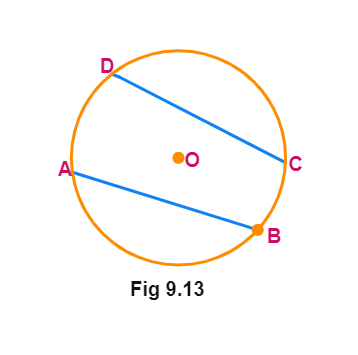
Given an arc PQ of a circle subtending angles POQ at the centre O and PAQ at a point A on the remaining part of the circle. We need to prove that ∠ POQ = 2 ∠ PAQ.
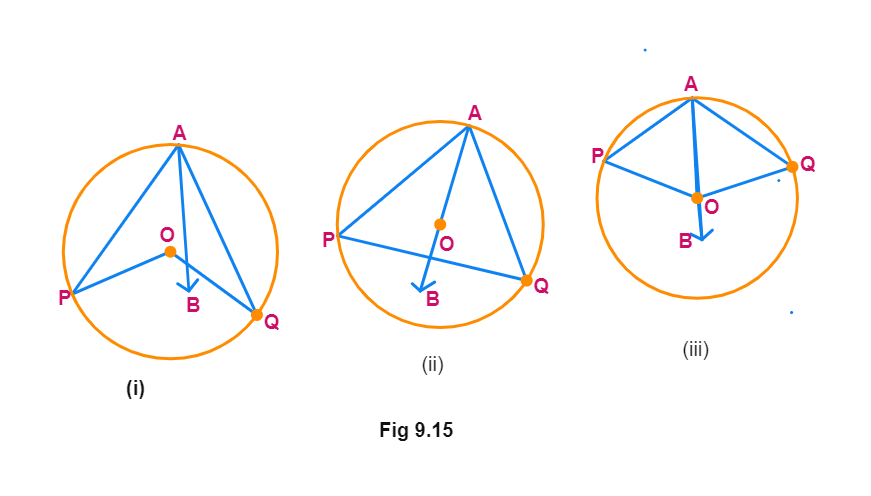
Consider the three different cases as given in above figure. In (i), arc PQ is minor; in (ii), arc PQ is a semicircle and in (iii), arc PQ is major. Let us begin by joining AO and extending it to a point B.
In all the cases, ∠ BOQ = ∠ OAQ + ∠ AQO because an exterior angle of a triangle is equal to the
Also in ∆ OAQ:
(i) OA =
which tells us that ∆ OAQ is an
i.e. ∠ OAQ = ∠
This gives ∠ BOQ = ∠ OAQ + ∠ OQA =
Similarly, ∠ BOP =
From (1) and (2), ∠ BOP + ∠ BOQ =
This is the same as ∠ POQ =
For the case (iii), where PQ is the major arc, (3) is replaced by:
reflex angle POQ =
Remark :
Suppose we join points P and Q and form a chord PQ in the above figures. Then ∠ PAQ is also called the angle formed in the segment PAQP.
In Theorem 9.7, A can be any point on the remaining part of the circle. So if you take any other point C on the remaining part of the circle, you have:
We observe from the above activity:
∠ POQ =
Therefore, ∠ PCQ = ∠
∠ POQ = 2 ∠
Again let us discuss the case (ii) of the theorem 9.7 separately.
Segment with ∠PAQ is a
According to the above theorem:
∠ POQ =
But from figure, PQ is the diameter therefore, ∠ POQ =
2 ∠ PAQ = 180°
∠ PAQ =
So, for any point on the semicircle (say, point C), again we get that: ∠ PCQ =
Therefore, you find another property of the circle as:
Angle in a semicircle is a right angle.
This proves the following:
Theorem 9.8
Angles in the Same Segment Theorem: Angles in the same segment of a circle are equal.
Given: ∠PAQ and ∠PCQ are angles in the same segment.
Construction: Join OP and OQ.
To Prove: ∠PAQ = ∠PCQ
Proof: From the above given figure, we can see that:
∠ POQ =
∠ POQ =
Therefore, ∠ PCQ = ∠
The converse of Theorem 9.8 is also true. A special case of the converse is stated as:
Theorem 9.9
Points Forming a Circle Theorem: If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).
Given: ∠ ACB = ∠ ADB
Construction: Extend the chord AD to a point outside the circle, say point E'.
To Prove: Points A, B,C and D all lie on the circumference of the circle.
Assumption: Suppose it does not pass through the point D. Then it will intersect AD (or extended AD) at a point, say E (inside the circle) or E′ (outside the circle).
Proof: Let us use proof by contradiction to prove the above theorem. So, we can say: ∠ ACB = ∠ AEB ( angles subtended by the
Therefore, ∠ AEB = ∠ ADB since, ∠ ACB = ∠ ADB.
This means that E needs to
Thus, points A,B,C and D (= E) will lie on the circumference of the circle i.e. the points are
Can this same argument be used for point E'?
This same argument can be used for point E′ as well where in order for ∠ ACB = ∠ AE'B to be true, point E' will have to coincide with point B.
