Perpendicular from the Centre to a Chord
Activity :
Draw a circle on a tracing paper. Let O be its centre. Draw a chord AB. Fold the paper along a line through O so that a portion of the chord falls on the other. Let the crease cut AB at the point M. Then, ∠ OMA = ∠ OMB =
or OM is perpendicular to AB.
Does the point B coincide with A?
Yes, it will. So MA =
Give a proof yourself by joining OA and OB and proving the right triangles OMA and OMB to be congruent. This example is a particular instance of the following result:
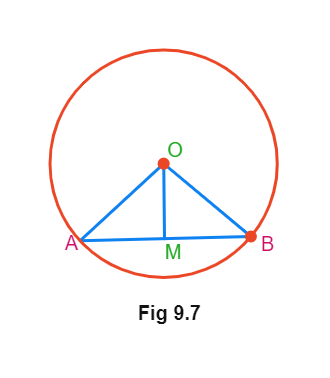
Theorem 9.3
Perpendicular Bisector from Centre Theorem: The perpendicular from the centre of a circle to a chord bisects the chord.
Given: OM is a perpendicular from the centre O i.e. ∠OMA = ∠OMB = 90°.
Construction: Join OA and OB.
To Prove: AM = BM
Proof: In the triangles △OMA and △OMB:
(i) OA = OB as they are
(ii) OM is
(iii) ∠OMA = ∠OMB =
Therefore, by
Thus, AM =
What about the converse of this theorem? Let's prove that as well. The converse is:
Theorem 9.4
Chord Bisector Perpendicular Theorem: The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Given: AM = BM
Construction: Join OA and OB.
To Prove: ∠OMA = ∠OMB = 90°
Proof: In the triangles △OMA and △OMB:
(i) OA = OB as they are
(ii) OM is
(iii) AM =
Therefore, by
Thus, by CPCT: ∠OMA = ∠
We also know that AB is a chord i.e.
