Cyclic Quadrilaterals
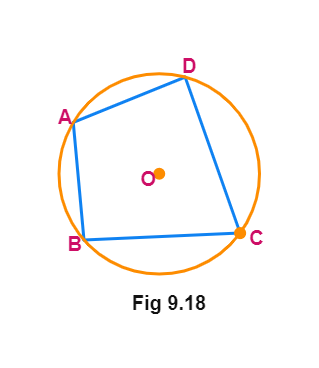
A quadrilateral ABCD is called
Note: Don't confuse between the terms: "con-cyclic" and "cyclic". The former is a concept related to a set of points while the latter is a specific property of a quadrilateral.
Activity:
You will find a peculiar property in such quadrilaterals. Draw several cyclic quadrilaterals of different sides and name each of these as ABCD. (This can be done by drawing several circles of different radii and taking four points on each of them.) Measure the opposite angles and write your observations in the following table.
${75}° + ${105}° =
Theorem 9.10
Angles in Cyclic Quadrilateral Theorem: The sum of either pair of opposite angles of a cyclic quadrilateral is 180º.
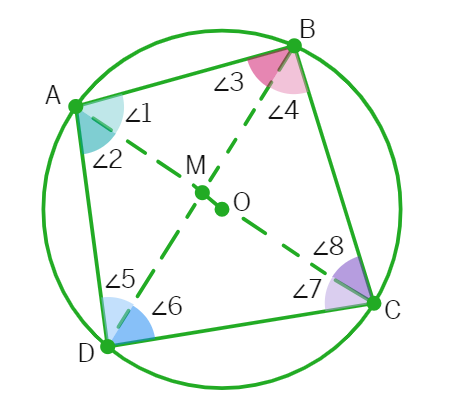
Given: ABCD is a cyclic quadrilateral of a circle with centre at O.
To prove: ∠BAD + ∠BCD = 180º and ∠ABC + ∠ADC = 180º
Proof: Consider each side of the quadrilateral. Each side is a
Thus, we can say:
(i) For Chord AB: ∠ 5 = ∠
For this same reason:
(ii) For Chord BC: ∠1 = ∠
(iii) For Chord CD: ∠2 = ∠
(iv) For Chord AD: ∠7 = ∠
From angle sum property of quadrilateral, we know: ∠A + ∠B + ∠C + ∠D =
Thus, ∠1 + ∠2 + ∠3 + ∠4 + ∠7 + ∠8 + ∠5 + ∠6 = 360º
Re-arranging, we get: (∠1 + ∠2 + ∠7 + ∠8) + (∠3 + ∠4 + ∠5 + ∠6) = 360º
(∠1 + ∠2 + ∠7 + ∠8) + (∠7 + ∠2 + ∠8 + ∠1) = 360º
From (1), (2) ,(3) and (4), we can further say:
∠1 + ∠2 + ∠7 + ∠8 =
(∠1 + ∠2) + (∠7 + ∠8) = 180º
∠BAD + ∠
Similarly, ∠ABC + ∠
Thus, the sum of either pair of opposite angles of a cyclic quadrilateral is 180º.
In fact, the converse of this theorem, which is stated below is also true.
Theorem 9.11
Cyclic Quadrilateral Theorem: If the sum of a pair of opposite angles of a quadrilateral is 180º, the quadrilateral is cyclic.
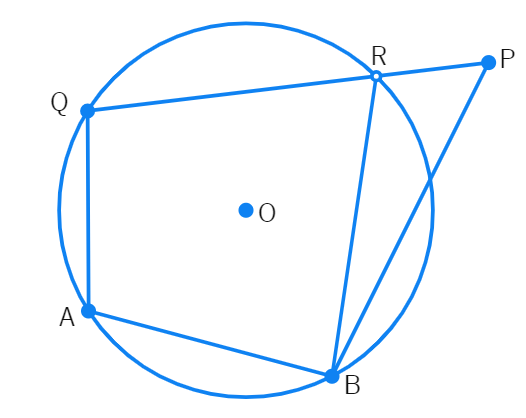
Given:
To Prove: The points A, B, P and Q lie on the circumference of a circle i.e. they are concyclic.
Proof: Consider a quadrilateral ABPQ, such that ∠ABP + ∠AQP = 180º and ∠QAB + ∠QPB = 180º
Assumption: Say point P does not lie on a circle drawn through points A, B and Q.
Construction: Let the circle cut QP at point R. Join BR.
∠QAB + ∠QRB =
∠QAB + ∠QPB =
∴ ∠QRB = ∠
But this cannot be true since ∠QRB = ∠QPB + ∠
∴ Our assumption that the circle does not pass through P is incorrect and A, B, P and Q lie on the circumference of a circle.
∴ ABPQ is a cyclic quadrilateral.
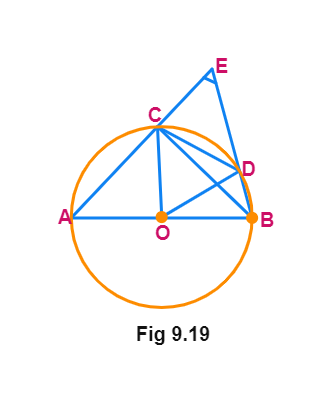
Example 2
In the figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠ AEB = 60°.
Solution
Join OC, OD and BC.
Triangle ODC is
Therefore, ∠ COD =
Now, ∠ CBD =
This gives ∠ CBD =
Again, ∠ ACB =
So, ∠ BCE =
Which gives ∠ CEB =
i.e., ∠ AEB = 60°
Example 3
In the figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠ DBC = 55° and ∠ BAC = 45°, find ∠ BCD.
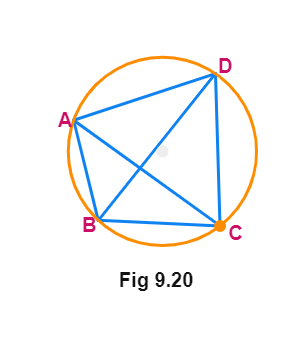
Solution
∠ CAD = ∠ DBC =
Therefore, ∠ DAB = ∠ CAD + ∠
But ∠ DAB + ∠ BCD =
So, ∠ BCD = 180° – 100° =
Example 4
Two circles intersect at two points A and B. AD and AC are diameters to the two circles. Prove that B lies on the line segment DC.
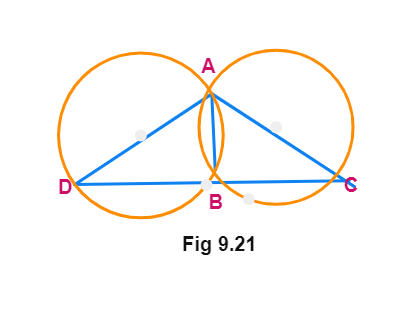
Solution Join AB.
∠ ABD =
∠ ABC =
So, ∠ ABD + ∠ ABC =
Therefore, DBC is a
Example 5
Prove that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic.
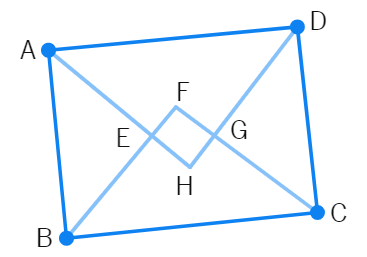
Solution
In the figure, ABCD is a quadrilateral in which the angle bisectors AH, BF, CF and DH of internal angles A, B, C and D respectively form a quadrilateral EFGH.
Now, ∠ FEH = ∠ AEB = 180° – ∠ EAB – ∠ EBA (sum of triangles is
=
and ∠ FGH = ∠ CGD = 180° – ∠ GCD – ∠
=
Therefore, ∠ FEH + ∠ FGH = 180° –
=
= 360° – 180° =
Hence, proved.
