Equal Chords and their Distances from the Centre
Here, we have a line AB and P is a point positioned above it. We know that there are
Now, let's take some random points lying on the line AB as shown below. If we join these points to P, we will get infinitely many such line segments. (PL1, PL2, PM, PL3, PL4 etc).
Which of these is the distance of AB from P?
Out of these line segments, the perpendicular from P to AB, namely PM in the below figure, will have the
In Mathematics, we define this least length PM to be the distance of AB from P.
So you may say that:
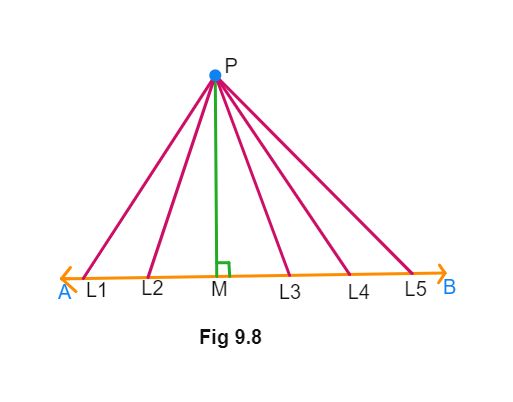
The length of the perpendicular from a point to a line is the distance of the line from the point.
Note that if the point lies on the line, the distance of the line from the point is zero. A circle can have infinitely many chords.
You may observe by drawing chords of a circle that longer chord is nearer to the centre than the smaller chord. You may observe it by drawing several chords of a circle of different lengths and measuring their distances from the centre.
What is the distance of the diameter, which is the longest chord from the centre?
Since the centre lies on it, the distance is zero. Do you think that there is some relationship between the length of chords and their distances from the centre? Let us see if this is so.
Activity :
Draw a circle of any radius on a tracing paper. Draw two equal chords AB and CD of it and also the perpendiculars OM and ON on them from the centre O. Fold the figure so that D falls on B and C falls on A [see Fig.9.9 (i)]. You may observe that O lies on the crease and N falls on M. Therefore, OM = ON.
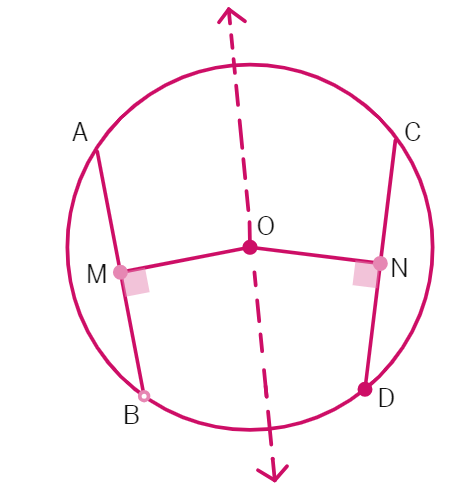
Repeat the activity by drawing congruent circles with centres O and O′ and taking equal chords AB and CD one on each. Draw perpendiculars OM and O′N on them. Cut one circular disc and put it on the other so that AB coincides with CD. Then you will find that O coincides with O′ and M coincides with N. In this way you verified the following:
Theorem 9.5
Equal Chords are Equidistant Theorem: Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
Given: AB and CD are equal chords of a circle.
Construction: Construct the Perpendiculars: Draw the perpendicular from O to AB and let it intersect AB at point M. Draw the perpendicular from O to CD and let it intersect CD at point N. Also join OA,OB, OC and OD.
To Prove: OM = ON
Proof: In order to prove- OM = ON: We have to prove that the four triangles: OMA, OMB , ONC and OND are congruent. In order to do this: We will prove △OMA ≅ △OMB , △ONC ≅ △OND , △OMA ≅ △ONC.
In the triangles △OMA and △OMB:
(i) ∠OMA = ∠OMB =
(ii) OA =
(iii) OM =
By the
Similarly, in the triangles △ONC and △OND:
(i) ∠ONC = ∠OND =
(ii) OC =
(iii) ON =
By the
Now, in the triangles △OMA and △ONC:
(i) ∠OMA = ∠ONC = 90° (as OM and ON are
(ii) OA =
(iii) AM =
By the
Result: Thus, we can conclude : OM = ON since that △OMA ≅ △OMB ≅ △ONC ≅ △OND.
Next, let's check whether the converse of this theorem is true or not. The converse of the Theorem 9.5 which is stated as follows:
Theorem 9.6
Equidistant Chords Equal Theorem: Chords equidistant from the centre of a circle are equal in length.
Given: Perpendiculars OM and ON are equal.
Construction: Join OA,OB, OC and OD.
To Prove: AB CD
Proof: In the triangles △OMA and △ONC:
(i) ∠OMA = ∠ONC =
(ii) OA =
(iii) OM =
By the
Thus, by CPCT: AM =
Since, perpendiculars drawn from the centre
Therefore, AM = BM = CN = DN. But AM + BM =
So, AB = CD.
We now take an example to illustrate the use of the above results:
Example 1: If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
Solution
Given that AB and CD are two chords of a circle, with centre O intersecting at a point E. PQ is a diameter through E, such that ∠ AEQ = ∠ DEQ. You have to prove that AB = CD.
Draw perpendiculars OL and OM on chords AB and CD, respectively. Now:
∠ LOE = 180° – 90° – ∠LEO =
= 90° – ∠AEQ = 90° – ∠DEQ = 90° – ∠MEO = ∠MOE
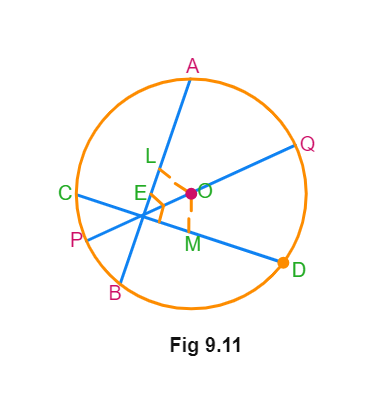
In triangles OLE and OME:
(i) ∠ LEO = ∠
(ii) ∠ LOE = ∠
(iii) EO =
Therefore, ∆ OLE ≅ ∆
This gives OL =
So, AB =
