More Patterns
Suppose we now want to make the letter C using the same sticks.
To make one C alphabet, we require
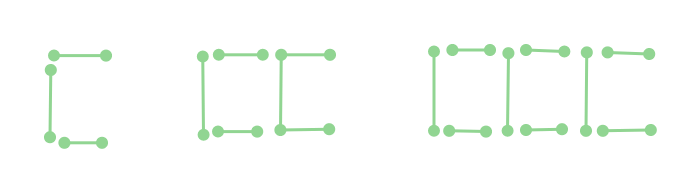
The table below gives the number of matchsticks required to make a repeated pattern of C for an 'n' number of Cs.
Can you figure out what are the correct answers for the blanks given?
| Number of Cs formed | Number of matchsticks used |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| 5 | 15 |
| 6 | |
| 7 | |
| 8 | |
| 11 | |
| 39 | |
As earlier, we now observe that:
Number of matchsticks required =
where 'n' is used for the number of Cs required and it takes all the possible values of
Simialrly, if we want to make a series of Fs like this :
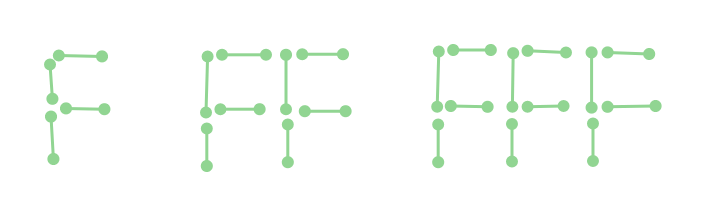
The generalized formula (if 'n' is the number of Fs to be made) becomes:
Number of matchsticks required =

Now, think of other alphabets and shapes that can be made from matchsticks.
Fill the number of sticks required for making one letter/shape
- U (
), - V (
), - triangle (
), - square (
)
