Simple Equations
Let us recall the face pattern.
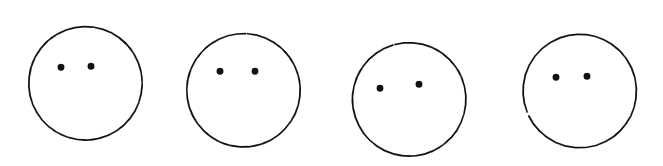
We know that the number of black stickers required is given by the rule
We can find the number of stickers required for a given number of faces. What about the other way?
We have to find the number of faces (i.e. m) for the given number of stickers
For 10 stickers we know 2m =
Observing the table:
| m | m | Condition Satisfied? Yes/No |
|---|---|---|
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 |
In an equation, there is always an equality sign. The equality sign shows that the value of the expression to the left of the sign (the left hand side or LHS) is
In the equation: (4x + 5) = 65, the LHS is (4x + 5) and the RHS is 65. In the equation: (10y – 20) = 50, the LHS is (10y – 20) and the RHS is 50.
If there is some sign other than the equality sign between the LHS and the RHS, it is not an equation.
Thus, 4x + 5 > 65 is not an equation. It says that, the value of (4x + 5) is greater than 65.
Similarly, 4x + 5 < 65 is not an equation. It says that the value of (4x + 5) is smaller than 65.
In equations, we often find that the RHS is just a number. But this need not be always so. The RHS of an equation may be an expression containing the variable.
For example, the equation:
4x + 5 = 6x – 25
has the expression (4x + 5) on the left and (6x – 25) on the right of the equality sign.
Thus,
(1) An equation is a condition on a variable. The condition is that two expressions should have equal value.
(2) Note that at least one of the two expressions must contain the variable.
We also note a simple and useful property of equations. The equation 4x + 5 = 65 is the same as 65 = 4x + 5. Similarly, the equation 6x – 25 = 4x +5 is the same as 4x + 5 = 6x – 25. An equation remains the same, when the expressions on the left and on the right are interchanged. This property is often useful in solving equations.
Consider the equation: 8 − 3 = 4 + 1.
What is the value of both the LHS and RHS ? Both have the value of
Let's try addition: Add 2 to both sides, which gives us
LHS: 8 − 3 + 2 =
RHS: 4 + 1 + 2 =
We see that the equality holds i.e. 7 = 7.
Thus, if we add the same number to both sides of an equality, the equality still holds.
Let's try subtraction: Subtract 2 from both sides, which gives us:
LHS : 8 − 3 − 2 =
RHS : 4 + 1 − 2 =
We see that the equality holds i.e. 3 = 3.
Thus, if we subtract the same number from both sides of an equality, the equality still holds.
Let's try multiplication: Multiply both the sides of the equality by 3, we get
LHS = 3 × (8 – 3) = 3 × 5 =
RHS = 3 × (4 + 1) = 3 × 5 =
We see that the equality holds i.e. 15 = 15.
Let's try division: Divide both sides of the equality by 2, we get
LHS = (8 – 3) ÷ 2 = 5 ÷ 2 =
RHS = (4+1) ÷ 2 = 5 ÷ 2 =
We see that the equality holds i.e.
Similarly, if we multiply or divide both sides of the equality by the same non-zero number, the equality still holds.
If we take any other equality, we shall find the same conclusions.
