Area
We have studied the areas of closed figures (regular and irregular) in previous grades. Let us recall some key points.
The amount of region enclosed by a closed figure is called its
In previous grades, we arrived at the formula for the area of a rectangle and a square using square grid paper. Do you remember?
Note : Help students in recalling the method of finding the area of a rectangle and a square using grid papers. Provide square grid papers to students and let them come up with the formula.
Example 1
1. A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution
Length of the floor =
Width of the floor =
Area of the floor = length × width = 5 m × 4 m =
Length of the square carpet =
Area of the carpet = length × length = 3 m × 3 m =
Hence, the area of the floor laid with carpet is 9 sq m.
Therefore, the area of the floor that is not carpeted is: area of the floor minus the area of the floor laid with carpet = 20 sq m – 9 sq m =
Example 2
2.Four square flower beds each of side 4 m are in four corners on a piece of land 12 m long and 10 m wide. Find the area of the remaining part of the land.
Solution
Length of the land (l) =
Width of land (w) =
Area of the whole land = l × w = 12 m × 10 m =
The sidelength of each of the four square flower beds is (s) =
Area of one flower bed = s × s = 4 m × 4 m =
Hence, the area of the four flower beds = 4 × 16 sq m =
Therefore, the area of the remaining part of the land is: area of the complete land minus the area of all four flower beds = 120 sq m – 64 sq m =
Example 1
1. The area of a rectangular garden 25 m long is 300 sq m. What is the width of the garden?
Solution
Length of the rectangular garden =
Area of the garden =
The formula for area of rectangle is Area = length x width.
Substituting values: 300 =
Solve for width: width = 300 ÷ 25 =
Example 2
2. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹8 per hundred sq m?
Solution
Length of the rectangular plot =
Width of the rectangular plot =
Cost of tiling = Rs 8 per 100 m²
The formula for area of rectangle is Area = length x width.
Substituting the given values: 500 x 200 =
Now, the cost of tilling the rectangular plot per hundred sq m. = ₹8
So, the cost of tiling 1,00,000 sq m. of land =
Therefore, the cost of tiling 1,00,000 sq m. of land is ₹ 8000
Example 3
3. A rectangular coconut grove is 100 m long and 50 m wide. If each coconut tree requires 25 sq m, what is the maximum number of trees that can be planted in this grove?
Solution
Length of the rectangular grove =
Width of the rectangular grove =
Area required for each tree =
The formula for area of rectangle is Area = length x width.
Substituting the given values: 100 x 50 =
Since each tree requires 25 m², the number of trees that can be planted is:
Maximum trees = 5,000 ÷ 25 =
The grove can accommodate 200 coconut trees.
Example 4
- By splitting the following figures into rectangles, find their areas (all measures are given in metres)
Example 1
1. Explore and figure out how many pieces have the same area.
Solution
Example 2
2.How many times bigger is Shape D as compared to Shape C? What is the relationship between Shapes C, D and E?
Solution
Example 3
3. Which shape has more area: Shape D or F? Give reasons for your answer.
Solution
Example 4
1. Which shape has more area: Shape F or G? Give reasons for your answer.
Solution
Look at the figures below and guess which one of them has a larger area.
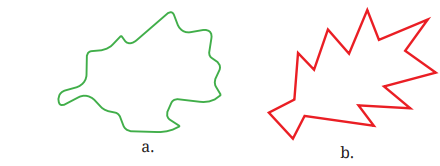
We can estimate the area of any simple closed shape by using a sheet of squared paper or graph paper where every square measures 1 unit × 1 unit or 1 square unit.
To estimate the area, we can trace the shape onto a piece of transparent paper and place the same on a piece of squared or graph paper and then follow the below conventions—
The area of one full small square of the squared or graph paper is taken as 1 sq unit.
Ignore portions of the area that are less than half a square.
If more than half of a square is in a region, just count it as 1 sq unit.
If exactly half the square is counted, take its area as
1 2
Find the area of the following figures.
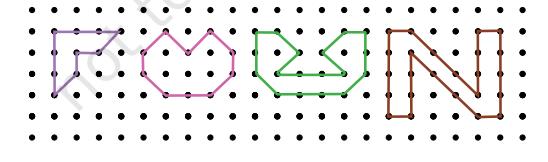
Let’s Explore!
Why is area generally measured using squares?
Draw a circle on a graph sheet with diameter (breadth) of length 3. Count the squares and use them to estimate the area of the circular region.
As you can see, circles can’t be packed tightly without gaps in between. So, it is difficult to get an accurate measurement of area using circles as units.
Here, the same rectangle is packed in two different ways with circles—the first one has 42 circles and the second one has 44 circles.
Try using different shapes (triangle and rectangle) to fill the given space (without overlaps and gaps) and find out the merits associated with using a square shape to find the area rather than another shape. List out the points that make a square the best shape to use to measure area.
1. Find the area (in square metres) of the floor outside of the corridor.
2. Find the area (in square metres) occupied by your school playground.
Let’s Explore!
On a squared grid paper (1 square = 1 square unit), make as many rectangles as you can whose lengths and widths are a whole number of units such that the area of the rectangle is 24 square units.
a. Which rectangle has the greatest perimeter?
b. Which rectangle has the least perimeter?
If you take a rectangle of area 32 sq cm, what will your answers be?
Given any area, is it possible to predict the shape of the rectangle with the greatest perimeter as well as the least perimeter? Give examples and reasons for your answer.
Area of a Triangle
Draw a rectangle on a piece of paper and draw one of its diagonals. Cut the rectangle along that diagonal and get two triangles.
Check! whether the two triangles overlap each other exactly.
Do they have the same area?
Try this with more rectangles having different dimensions. You can check this for a square as well.
Can you draw any inferences from this exercise? Please write it here.
Now, see the figures below. Is the area of the blue rectangle more or less than the area of the yellow triangle? Or is it the same? Why?
Can you see some relationship between the blue rectangle and the yellow triangle and their areas? Write the relationship here.
Note: Help students in articulating their inferences and in defining the relationships they have observed in their own words, gradually leading to a common statement for whole classroom. Recall the definition of a diagonal in the classroom.
Draw suitable triangles on grid paper to verify your inferences and relationships observed in the above exercises.
Use your understanding from previous grades to calculate the area of any closed figure using grid paper and
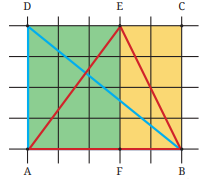
1. Find the area of blue triangle BAD
2. Find the area of red triangle ABE.

Area of rectangle ABCD =
So, the area of triangle BAD is half of the area of the rectangle ABCD.
Area of triangle ABE = Area of triangle AEF + Area of triangle BEF.
Here, the area of triangle AEF = half of the area of rectangle AFED.
Similarly, the area of triangle BEF = half of the area of rectangle BFEC.
Thus, the area of triangle ABE = half of the area of rectangle AFED +half of the area of rectangle BFEC
= half of the sum of the areas of the rectangles AFED and BFEC = half of the area of rectangle ABCD.
- Find the areas of the figures below by dividing them into rectangles and triangles.
Making it ‘More’ or ‘Less’
Observe these two figures. Is there any similarity or difference between the two?
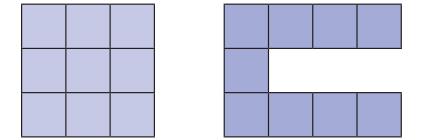
Using 9 unit squares (having an area of 9 sq units), we have made figures with two different perimeters—the first figure has a perimeter of 12 units and the second has a perimeter of 20 units.
Arrange or draw different figures with 9 sq units to get other perimeters. Each square should align with at least one other square on at least one side completely and together all squares should form a single connected figure with no holes.
Using 9 unit squares, solve the following.
1. What is the smallest perimeter possible?
2. What is the largest perimeter possible?
3. Make a figure with a perimeter of 18 units.
4. Can you make other shaped figures for each of the above three perimeters, or is there only one shape with that perimeter?
What is your reasoning?
Let’s do something tricky now! We have a figure below having perimeter 24 units.
Without calculating all over again, observe, think and find out what will be the change in the perimeter if a new square is attached as shown on the right.
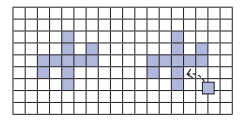
Experiment placing this new square at different places and think what the change in perimeter will be. Can you place the square so that the perimeter: a) increases; b) decreases; c) stays the same? Below is the house plan of Charan. It is in a rectangular plot. Look at the plan. What do you notice?
Some of the measurements are given. a. Find the missing measurements. b. Find out the area of his house.
Now, find out the missing dimensions and area of Sharan’s home. Below is the plan:
Some of the measurements are given. a. Find the missing measurements. b. Find out the area of his house. What are the dimensions of all the different rooms in Sharan’s house? Compare the areas and perimeters of Sharan’s house and Charan’s house.
Area Maze Puzzles
In each figure, find the missing value of either the length of a side or the area of a region.
Example 1
1. Give the dimensions of a rectangle whose area is the sum of the areas of these two rectangles having measurements: 5 m × 10 m and 2 m × 7 m.
Solution
The dimensions of a rectangle whose area is the sum of the areas of these two rectangles having measurements.
The areas of the rectangles are:
Area 1 = 5 × 10 =
Area 2 = 2 × 7 =
Total Area = 50 + 14 =
Dimensions can be
Example 2
1. The area of a rectangular garden that is 50 m long is 1000 sq m. Find the width of the garden.
Solution
The area of the garden is 1000 square meters. Using the formula:
The area of a rectangle formula: Area = Length × Width
Length =
Area =
Width = Area ÷ Length
Width = 1000 ÷ 50 =
The width of the garden is 20 meters.
Example 3
3. The floor of a room is 5 m long and 4 m wide. A square carpet whose sides are 3 m in length is laid on the floor. Find the area that is not carpeted.
Solution
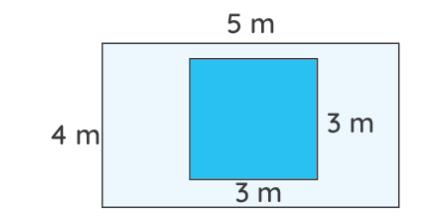
Area of the floor = length × breath
Area of the floor = 5 ×
=
The carpet is square, so its area is: Area = side × side
Area of the square carpet = 3 ×
=
Now, we will be subtracting the square carpet area from the floor's area to get the area of the floor that is not carpeted.
Hence, the area of the floor that is not carpeted = 20 – 9 =
Thus, the area of the floor that is not carpeted is 11
Example 4
4. Four flower beds having sides 2 m long and 1 m wide are dug at the four corners of a garden that is 15 m long and 12 m wide. How much area is now available for laying down a lawn?
Solution
The garden is a rectangle, so its area is: Area = length × width
4 flower beds having sides 2 m long and 1 m wide are dug at the four corners of a garden that is 15 m long and 12 m wide.
Garden area = 15 ×
Area of one flower bed = 2 × 1 =
Area of four flower beds = 4 × 2 =
Remaining area = 180 − 8 =
Example 5
5. Shape A has an area of 18 square units and Shape B has an area of 20 square units. Shape A has a longer perimeter than Shape B. Draw two such shapes satisfying the given conditions.
Solution
A has an area of 18 square units and Shape B has an area of 20 square units, Shape A has a longer perimeter than Shape B.
Shape A: Dimensions = 1 × 18,
Area =
Perimeter =
Shape B: Dimensions = 4 × 5,
Area =
Shape A has a longer perimeter than Shape B.
Example 6
6. On a page in your book, draw a rectangular border that is 1 cm from the top and bottom and 1.5 cm from the left and right sides. What is the perimeter of the border?
Solution
A page in your book, draw a rectangular border that is 1 cm from the top and bottom and 1.5 cm from the left and right sides.
Reduced Length = Original Length − 2
Reduced Width = Original Width − 3
Perimeter = 2 × (Reduced Length + Reduced Width).
Substitute the original dimensions to find the perimeter of the border.
Example 7
7. Draw a rectangle of size 12 units × 8 units. Draw another rectangle inside it, without touching the outer rectangle that occupies exactly half the area.
Solution
The total area of the outer rectangle is
Half this area is
The inner rectangle could be 8 units ×
Example 8
8. A square piece of paper is folded in half. The square is then cut into two rectangles along the fold. Regardless of the size of the square, one of the following statements is always true. Which statement is true here?
a. The area of each rectangle is larger than the area of the square.
b. The perimeter of the square is greater than the perimeters of both the rectangles added together.
c. The perimeters of both the rectangles added together is always 1
d. The area of the square is always three times as large as the areas of both rectangles added together.
Solution
The perimeters of both rectangles added together are always 1.5 times the perimeter of the square. This is because folding creates two rectangles with lengths equal to half the square. Option (C) is correct.
