Exercise 10.1
1. Find the perimeter of each of the following shapes :
(i) Shape 1:
Given that AB =
Perimeter of shape 1 =
=
(ii) Shape 2 :
Given that
AB =
AB = HG =
GF =
GF = HI =
ED =
ED = JK =
IJ =
IJ = LK =
AL =
AL = BC =
CD =
CD = EF =
Perimeter of shape 2 = AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA
=
=
(iii) Shape 3 :
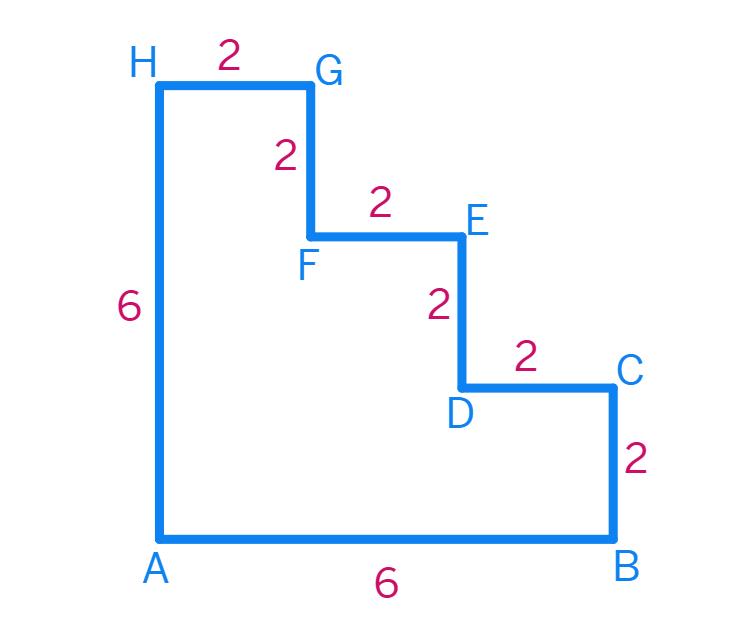
Given that
AB =
CD =
EF =
GH =
Perimeter of shape 3 = AB + BC + CD + DE + EF + FG + GH + HA
= (
=
(iv) Shape 4 :
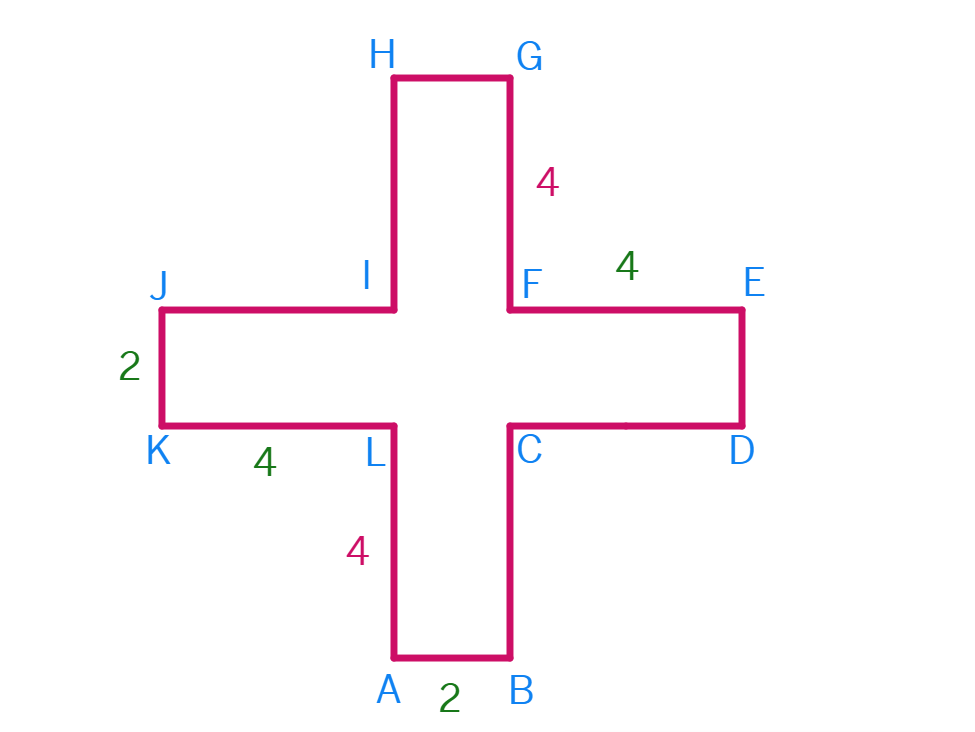
Given that
AL =
AB =
AB = HG =
JK =
JK = ED =
GF =
GF = HI =
KL =
KL = IJ =
EF =
EF = CD =
Perimeter of shape 4 = AB + BC + CD + DE + EF + FG + GH + HI + IJ + JK + KL + LA
=
=
Find the area of each of the following triangles.
What would be cost of putting a wire around each of these shapes given that 1 cm wire costs ₹ 15 ?
(i)
Solution:
(i)
Perimeter = AB + BC +
=
=
(ii)
Solution:

(ii)
ABCD is a rectangle, so opposite sides are equal.
Perimeter = AB +
=
Cost of putting a wire around the given shape at Rs.
=
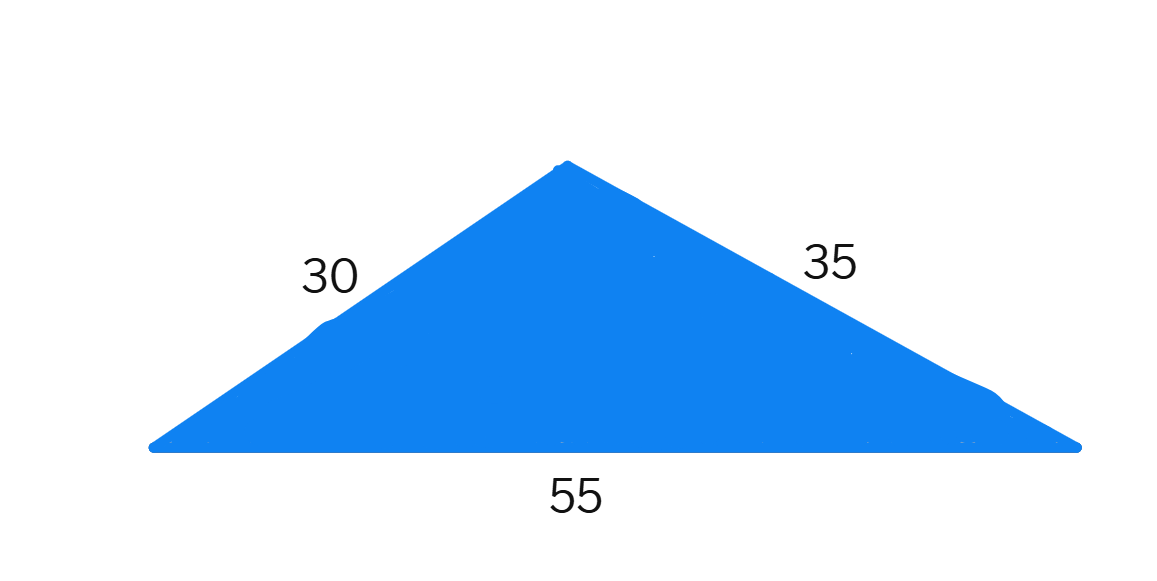
(iii)
Solution:
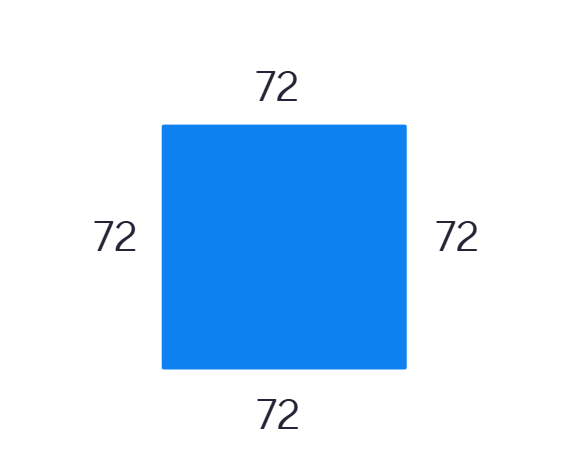
(iii)
ABCD is a square, so all sides are
Perimeter =
=
Perimeter =
Cost of putting a wire around the given shape at Rs.
=
Therefore Cost = Rs.
(iv)
Solution:
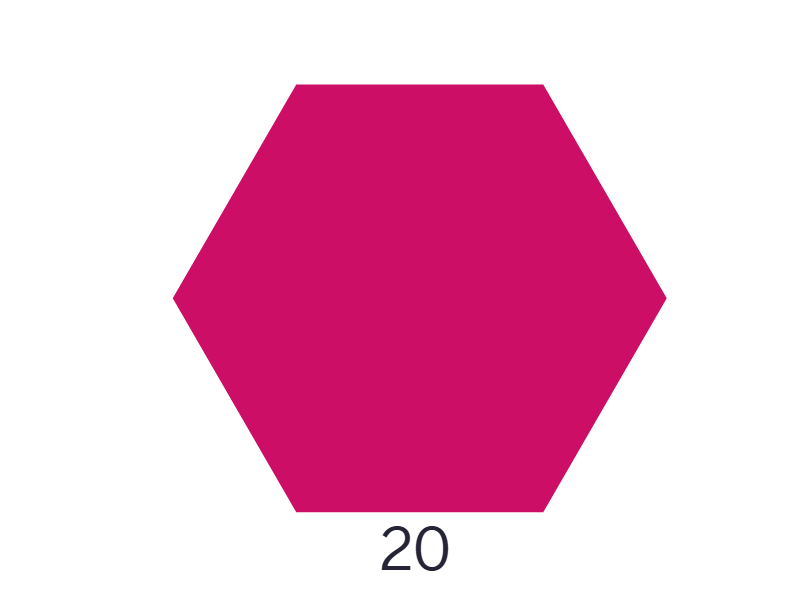
(iv)
ABCDEF is a regular
Perimeter = 6 × side
=
Perimeter =
Cost of putting a wire around the given shape at Rs.
=
Therefore cost = Rs.
3. How many different rectangles can you make with a 24 cm long string with integral sides and what are the sides of those rectangles in cm?
Solution:
The length of the string =
Perimeter of the rectangle = 2(l + b) =
l + b = 24/2 =
We can make different rectangles with a 24 cm long string as follows:
| S.No. | Length in cm | Breadth in cm | Perimeter of the rectangle = 24 cm |
|---|---|---|---|
| 1 | 1 | 2(1 + 11) = 2 × | |
| 2 | 2 | 2(2 + 10) = 2 × | |
| 3 | 3 | 2(3 + 9) = 2 × | |
| 4 | 4 | 2(4 + 8) = 2 × | |
| 5 | 5 | 2(5 + 7) = 2 × | |
| 6 | 7 | 2(7 + 5) = 2 × | |
| 7 | 8 | 2(8 + 4) = 2 × | |
| 8 | 9 | 2(9 + 3) = 2 × |
Thus, there are
A flower bed is in the shape of a square with a side of 3.5 m. Each side is to be fenced with 4 rows of ropes. Find the cost of rope required at ₹ 15 per meter.
Solution:
The shape of the flower bed is a
The length of the side of the square =
Length of 4 rows of ropes on each side = 4 × 3.5 m =
Total length of the rope on all 4 sides = 14 m × 4 =
Cost of rope required at ₹ 15 per meter = 56 × 15 = ₹
Thus, the total cost of the rope required is ₹
5. A piece of wire is 60 cm long. What will be the length of each side if the string is used to form :
(i)
(i) an equilateral triangle
Solution:
Length of the wire =
The perimeter of an equilateral triangle with side
3x =
x =
Length of each side of the equilateral triangle is 20 cm
(ii)
(ii) A Square
Solution:
Length of the wire =
The perimeter of a square with side
4x =
x =
Length of each side of the square is 15 cm
(iii)
(iii) A Regular Hexagon
Solution:
Length of the wire =
The perimeter of a regular hexagon with side
6x =
x =
Length of each side of the regular hexagon is 10 cm
(iv)
(iv) A Regular Pentagon
Solution:
Length of the wire =
The perimeter of a regular pentagon with side
5x =
x =
Length of each side of the regular pentagon is 12 cm
6. Bunty and Bubly go for jogging every morning. Bunty goes around a square park of side 80 m. Bubly goes around a rectangular park with length 00 m and breadth 60 m. If they both fake 3 rounds, who covers more distance and by how much ?
Bunty and Bubly Jogging Distance
Solution:
Bunty goes around a square park.
The length of the side of the square park =
The perimeter of the square park = 4 ×
Distance covered by Bunty in 3 rounds =
Bubly goes around a rectangular park.
The length and breadth of the park are
The perimeter of the rectangular park = 2 × (length + breadth)
= 2 × (
= 2 ×
Distance covered by Bubly in 3 rounds =
Comparison:
Bunty covers a greater distance than
Extra distance covered by Bunty =
7. The length of a rectangle is twice of its breadth. If its perimeter is 48 cm, find the dimensions of the rectangle.
Solution:
The perimeter of the rectangle =
Let the breadth of the rectangle be
The length of the rectangle = 2 ×
Perimeter of the rectangle = 2 × (length + breadth)
= 2 × (
= 2 × 3x =
By problem, 6x =
x =
Breadth of the rectangle = 8 cm
Length of the rectangle = 2 × 8 =
Two sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is the length of third side ?
Solution:
Two sides of a triangle are
Let the third side be
Perimeter of the triangle =
=
By problem, 26 + x =
x =
Therefore Length of the third side of the triangle is 10 cm
Find the perimeter of each of the following shapes:
Solution:
(i)
(i) A triangle of sides 3 cm., 4 cm. and 5 cm.
Solution:
Perimeter of a Triangle
The sides of the triangle are
Perimeter of the given triangle =
= 3 + 4 + 5 =
Therefore the perimeter of the given triangle is 12 cm.
(ii)
(ii) An equilateral triangle of side 9 cm.
Solution:
Perimeter of an Equilateral Triangle
Side of the equilateral triangle =
Perimeter of the equilateral triangle = 9 + 9 + 9 =
Therefore all three sides are
(iii)
(iii) An isosceles triangle with equal sides 8 cm each and third side of 6 cm.
Solution:
Perimeter of an Isosceles Triangle
The length of one of the equal sides of the isosceles triangle =
Length of the third side =
Perimeter of the given triangle = 8 + 8 + 6 cm =
Therefore the area of the given triangle is 22 cm.
