Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Symmetry

    Introduction

    Line Symmetry

    Rotational Symmetry

    Line Symmetry and Rotational Symmetry

    Exercise 15.1

    Exercise 15.2

    Exercise 15.3

    Exercise 15.4

    Looking Back

    Easy Level Worksheet

    Moderate Level Worksheet

    Hard Level Worksheet

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Symmetry > Rotational Symmetry

Rotational Symmetry

What do you say when the hands of a clock go round?

You say that they rotate. The hands of a clock rotate in only direction, about a fixed point, the centre of the clock-face.

Rotation, like movement of the hands of a clock, is called a clockwise rotation; otherwise it is said to be anticlockwise.

What can you say about the rotation of the blades of a ceiling fan? It rotates in a direction.

If you spin the wheel of a bicycle, it rotates. It can rotate in either way: both clockwise and anticlockwise.

When an object rotates, its shape and size do not change. The rotation turns an object about a fixed point. This fixed point is the centre of rotation.

The angle of turning during rotation is called the angle of rotation. A full turn, you know, means a rotation of 360°.

A half-turn means rotation by °; a quarter-turn is rotation by °. When it is 12 o’clock, the hands of a clock are together. By 3 o’clock, the minute hand would have made three complete turns; but the hour hand would have made only a quarter-turn. What can you say about their positions at 6 O’clock?

We can rotate this paper wind mill, and it looks the same afterwards. We say that it has rotational symmetry.

Have you ever made a paper windmill? The Paper windmill in the picture looks symmetrical but you do not find any line of symmetry. No folding can help you to have coincident halves. However if you rotate it by 90° about the fixed point, the windmill will look exactly the same. We say the windmill has a symmetry.

In a full turn, there are precisely four positions (on rotation through the angles 90°, 180°, 270° and 360°) when the windmill looks exactly the same. Because of this, we say it has a rotational symmetry of order 4. Here is one more example for rotational symmetry.

Consider a square with A,B,C,D as of its corners.

Let us perform quarter-turns about the centre of the square marked x.

Thus a square has a rotational symmetry of order 4 about its centre. Observe that in this case,

(i) The centre of rotation is the of the square.

(ii) The angle of rotation is °.

(iii) The direction of rotation is .

(iv) The order of rotational symmetry is .

The point where we have the pin is the centre of rotation. It is the intersecting point of the diagonals in this case.

Every object has a rotational symmetry of order , as it occupies same position after a rotation of 360° (i.e., one complete revolution). Such cases have no interest for us.

You have around you many shapes, which possess rotational symmetry

For example, when you slice certain fruits, the cross-sections are shapes with rotational symmetry. This might surprise you when you notice them

1.(a) Can you now tell the order of the rotational symmetry for an equilateral triangle? (Fig)

In a full turn, there is precisely three-position (on rotation through the angles 120°, 240°, and 360°) when the triangle looks exactly the same. Because of this, we can say that it has rotational symmetry of order .

(b) How many positions are there at which the triangle looks exactly the same, when rotated about its centre by 120°?

There is only one position where the triangle looks exactly the when rotated about its centre.

2. Which of the following shapes (Fig) have rotational symmetry about the marked point.

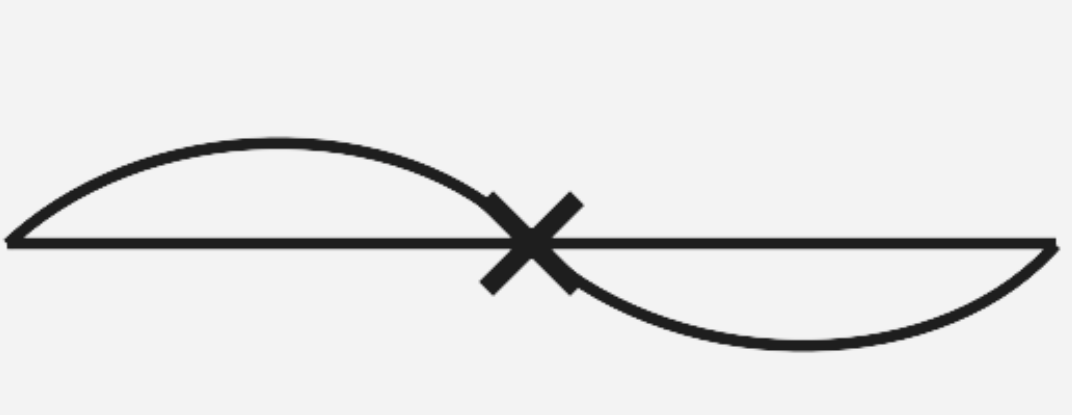
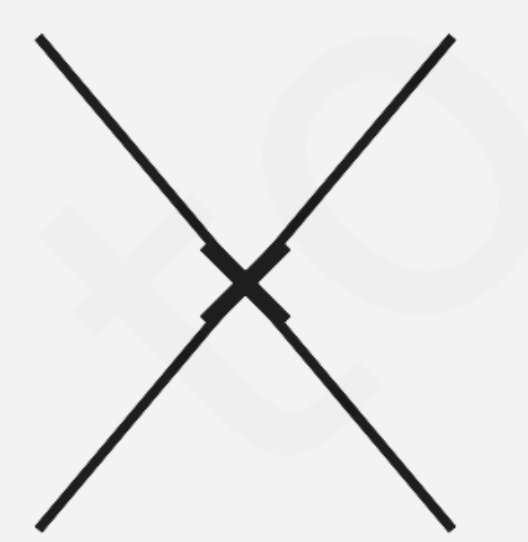
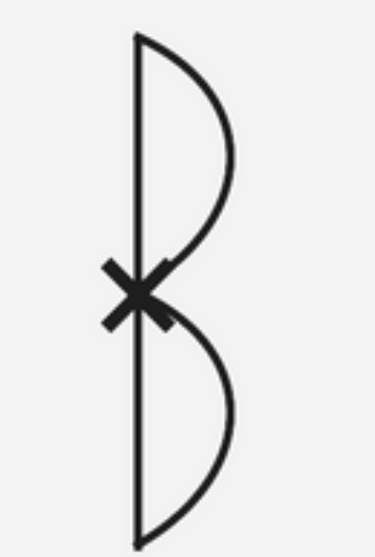
We know that when a figure which on rotation through an angle, about a point, look the same as the original, is said to have rational symmetry. Figures (i), (ii), (iii) and () have rotational symmetry.

Give the order of the rotational symmetry of the given figures about the point marked x.

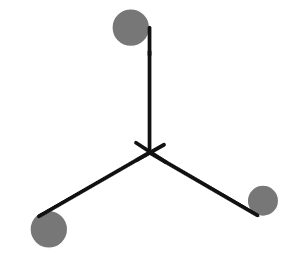
(i)

(ii)

(iii)