Exercise 12.2

1. In the figure, if AB = CD and ∠AOB = 90°, find ∠COD.

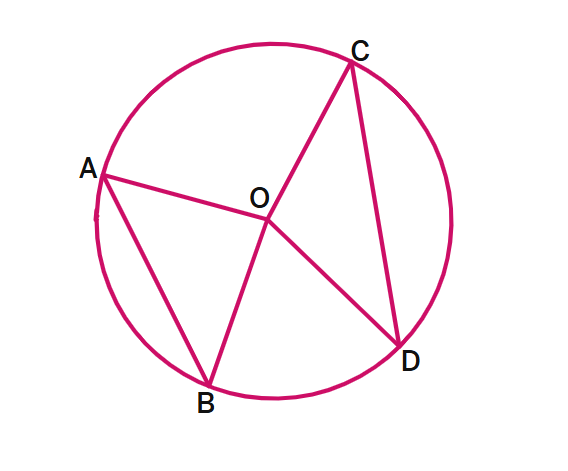
Solution:

Given: AB = CD and ∠AOB = °

Since AB and CD are equal chords of the same circle:

Equal chords subtend angles at the centre.

Therefore: ∠AOB =

Since ∠AOB = 90°:

∠COD = °

2. In the figure, PQ = RS and ∠QRS = 48°. Find ∠OPQ and ∠ROS.

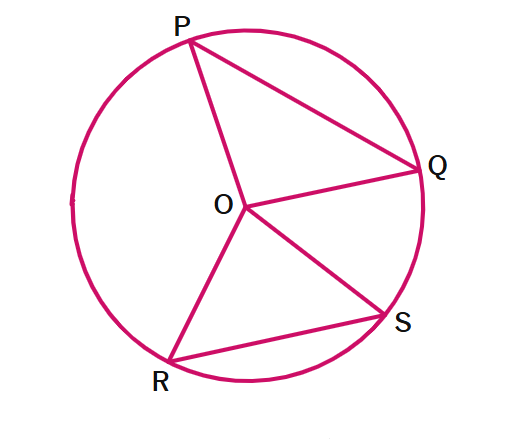
Solution:

Given: PQ = RS and ∠QRS = °

Since PQ = RS (equal chords):

Equal chords subtend angles at the centre.

Therefore: ∠POQ =

Since ∠QRS is an inscribed angle and ∠ROS is the central angle subtending the same arc RS:

Central angle = × inscribed angle

∠ROS = 2 × ∠QRS = 2 × ° = °

Since ∠POQ = ∠ROS:

∠POQ = °

In triangle OPQ, OP = OQ ( of circle)

So triangle OPQ is

∠OPQ = ∠OQP = (180° - ∠POQ)/2 = (180° - °)/2 = °

3. In the figure PR and QS are two diameters. Is PQ = RS?

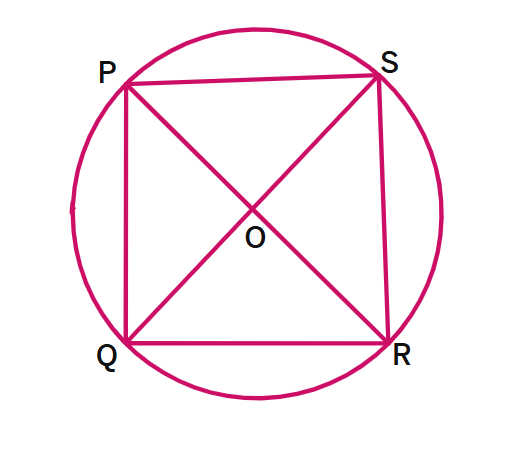
Solution:

Given: PR and QS are of the circle

Since both are diameters, they pass through the O.

In the circle:

PO = OR = (since PR is a diameter)

QO = OS = (since QS is a diameter)

All radii of a circle are :

PO = QO = RO = SO =

In triangles POQ and ROS:

PO = = r

QO = = r

∠POQ = (vertically opposite angles)

By congruence: ΔPOQ ≅ ΔROS

Therefore: PQ =

Answer: Yes, PQ = RS