Exercise 12.4

1. In the figure, 'O' is the centre of the circle. ∠AOB = 100°, find ∠ADB.

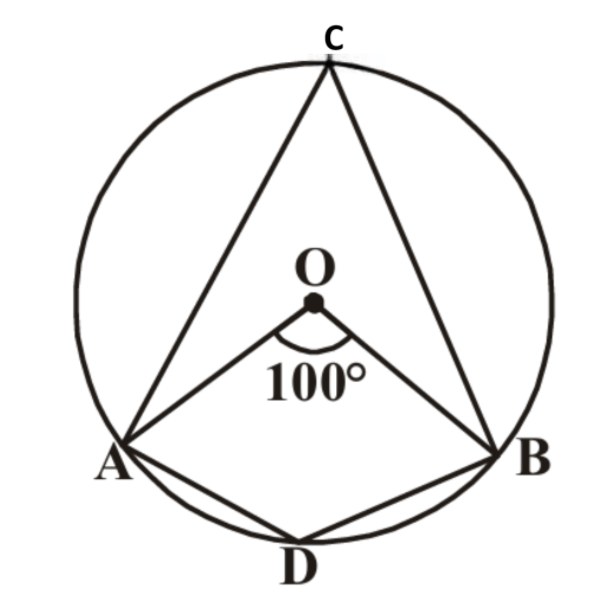
Solution:

Given: ∠AOB = °

∠AOB is the angle subtending arc AB.

∠ADB is the angle subtending the same arc AB.

By the inscribed angle theorem:

Inscribed angle = × central angle

∠ADB = × ∠AOB = × ° = °

2. In the figure, ∠BAD = 40°, then find ∠BCD.

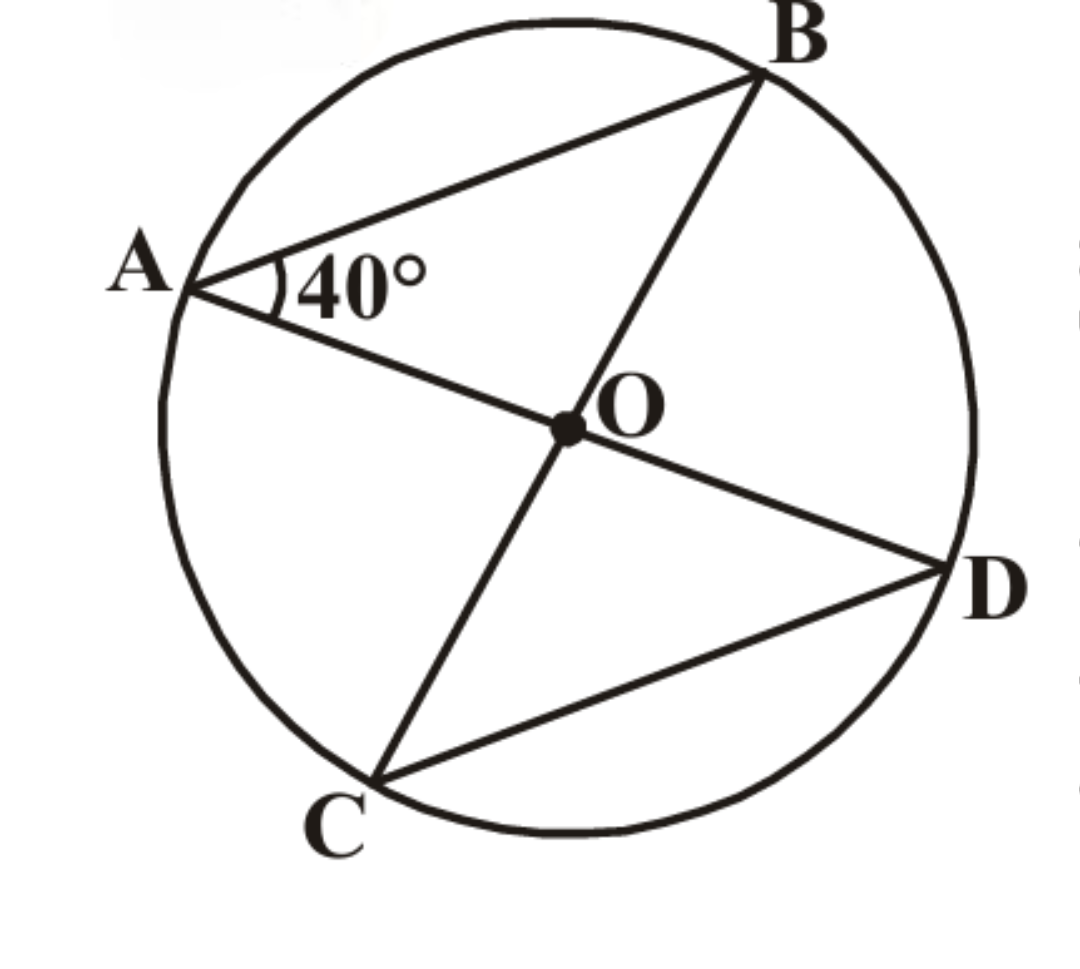
Solution:

Given: ∠BAD = °

ABCD is a quadrilateral (inscribed in a circle).

In a cyclic quadrilateral, opposite angles are .

Therefore: ∠BAD + ∠BCD = °

° + ∠BCD = 180°

∠BCD = 180° - ° = °

3. In the figure, O is the centre of the circle and ∠PQR = 120°. Find ∠POR and ∠PSR.

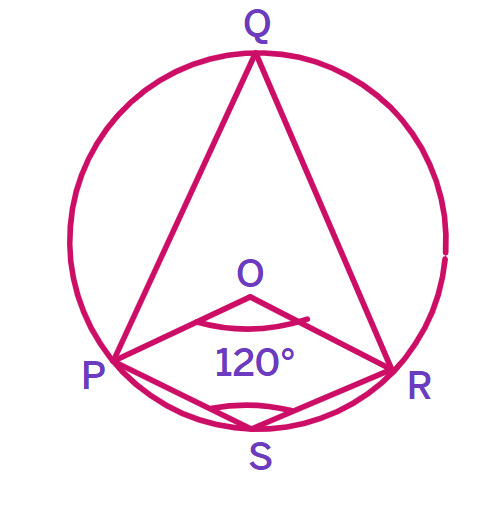
Solution:

Given: ∠PQR = °

Finding ∠POR:

∠PQR is an angle subtending arc PR.

∠POR is the angle subtending the same arc PR.

Central angle = × inscribed angle

∠POR = 2 × ∠PQR = 2 × ° = °

Since 240° > 180°, we take the reflex angle.

The actual ∠POR = 360° - 240° = °

Finding ∠PSR:

Both ∠PQR and ∠PSR are inscribed angles subtending the same arc .

Inscribed angles subtending the same arc are .

Therefore: ∠PSR = ∠PQR = °

4. In the figure, 'O' is the centre of the circle. OM = 3cm and AB = 8cm. Find the radius of the circle.

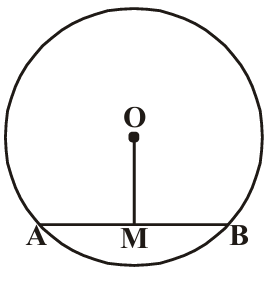
Solution:

Given: OM = cm and AB = cm

OM is to chord AB (from the figure).

The perpendicular from centre to a chord the chord.

Therefore: AM = MB = AB/2 = /2 = cm

In right triangle OMA:

OA² = OM² + AM² (Pythagorean theorem)

OA² = ² + ² = + =

OA = √ = cm

Since OA is a radius: radius = cm

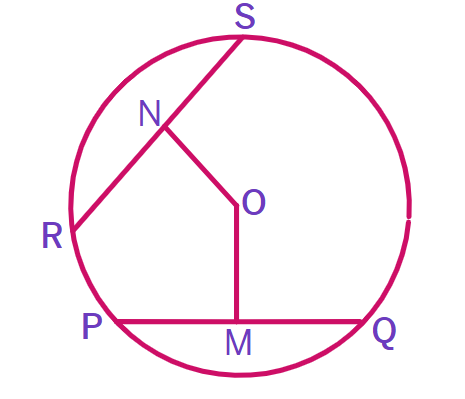
5. In the figure, 'O' is the centre of the circle and OM, ON are the perpendiculars from the centre to the chords PQ and RS. If OM = ON and PQ = 6cm. Find RS.

Solution:

Given: OM ⊥ PQ, ON ⊥ RS, OM = , and PQ = cm

Since OM = ON:

The chords PQ and RS are from the centre.

Theorem: Chords equidistant from the centre are in length.

Therefore: PQ =

Since PQ = 6 cm:

RS = cm

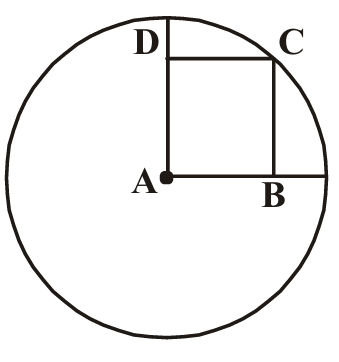
6. A is the centre of the circle and ABCD is a square. If BD = 4cm then find the radius of the circle.

Solution:

Given: A is the centre, ABCD is a , BD = cm

In square ABCD, the diagonals are and bisect each other at right angles.

Since A is the centre of the circle and also the centre of square ABCD:

All vertices B, C, D are equidistant from A.

Therefore: AB = AC = AD =

In a square, if side length is s, then diagonal = s√

Let the side length of square = s

Then diagonal BD = s√2 = cm

s = /√2 = /√2 × √2/√2 = 4√2/2 = cm

The radius = side length of square = cm ≈ cm

7. Draw a circle with any radius and then draw two chords equidistant from the centre.

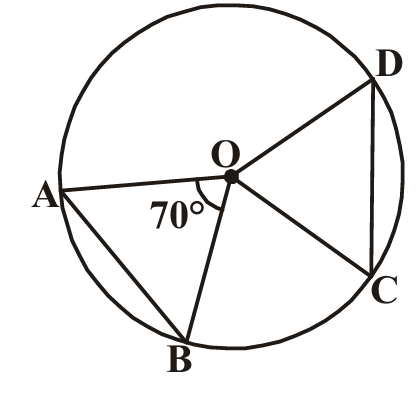
8. In the given figure 'O' is the centre of the circle and AB, CD are equal chords. If ∠AOB = 70°. Find the angles of the ΔOCD.

Solution:

Given: AB = CD (equal chords) and ∠AOB = °

Since AB = CD are equal chords:

Equal chords subtend central angles.

Therefore: ∠AOB = = °

In triangle OCD:

OC = OD = of the circle

Therefore, triangle OCD is .

In an isosceles triangle, base angles are .

Let ∠OCD = ∠ODC = x

Sum of angles in triangle = °

∠COD + ∠OCD + ∠ODC = 180°

° + x + x = 180°

70° + 2x = 180°

2x = °

x = °

Therefore: ∠COD = °, ∠OCD = °, ∠ODC = °