Exercise 12.3

1. Draw the following triangles and construct circumcircles for them.

(i) In ΔABC, AB = 6cm, BC = 7cm and ∠A = 60°

(ii) In ΔPQR, PQ = 5cm, QR = 6cm and RP = 8.2cm

(iii) In ΔXYZ, XY = 4.8cm, ∠X = 60° and ∠Y = 70°

2. Draw two circles passing through A, B where AB = 5.4cm

Solution:

Steps for construction:

1. Draw line segment AB = cm

2. Draw the perpendicular bisector of AB

3. Mark any point on this perpendicular bisector

4. With C as centre and CA as radius, draw the circle

5. This circle passes through both and

6. Mark another point on the perpendicular bisector

7. With D as centre and DA as radius, draw the circle

8. This circle also passes through both A and B

Note: Any circle passing through two points must have its centre on the of the line segment joining those points.

3. If two circles intersect at two points, then prove that their centres lie on the perpendicular bisector of the common chord.

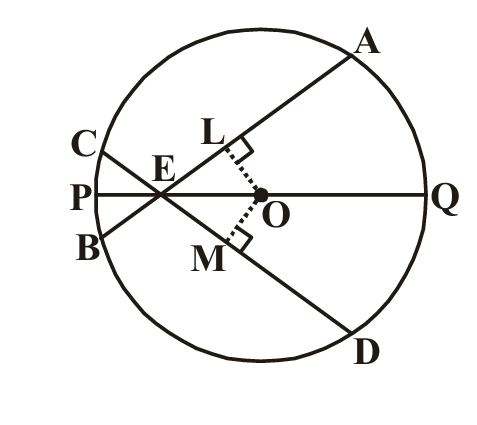
Solution:

Let the two circles with centres O₁ and O₂ intersect at points and .

AB is the of both circles.

To prove: O₁ and O₂ lie on the perpendicular bisector of AB

Proof:

Since A and B are points on the circle with centre O₁:

O₁A = (radii of the same circle)

Therefore, O₁ is from A and B

Similarly, since A and B are points on the circle with centre O₂:

O₂A = (radii of the same circle)

Therefore, O₂ is also from A and B

The locus of all points equidistant from two given points is the of the line segment joining them.

Since both O₁ and O₂ are equidistant from A and B:

Both O₁ and O₂ lie on the of AB.

Hence proved.

4. If two intersecting chords of a circle make equal angles with diameter passing through their point of intersection, prove that the chords are equal.

Solution:

Let AB and CD be two chords intersecting at point .

Let EF be the diameter passing through P.

Given: ∠APE = (or equal angles with the diameter)

To prove: AB =

Proof:

Draw perpendiculars from centre O to chords AB and CD.

Let OM ⊥ AB and ON ⊥ CD.

Since the perpendicular from centre bisects the chord:

AM = and CN =

In the configuration, since the chords make equal angles with the diameter:

The perpendicular distances from centre O to both chords are .

Therefore: OM =

Chords equidistant from the centre are in length.

Therefore: AB =

Hence proved.

5. In the adjacent figure, AB is a chord of circle with centre O. CD is the diameter perpendicular to AB. Show that AD = BD.

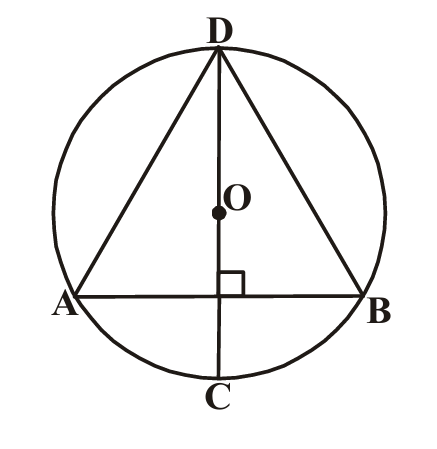
Solution:

Given: AB is a chord, CD is diameter ⊥ AB

To prove: AD =

Proof:

Since CD is perpendicular to chord AB:

CD the chord AB (perpendicular from centre bisects the chord)

Let CD intersect AB at point .

Then: AM =

In triangles AMD and BMD:

AM = (proved above)

DM = (common side)

∠AMD = ∠ = 90° (given that CD ⊥ AB)

By congruence: ΔAMD ≅ ΔBMD

Therefore: AD = (corresponding parts of congruent triangles)

Hence proved.