Exercise 12.5
1. Find the values of x and y in the figures given below.
(i)
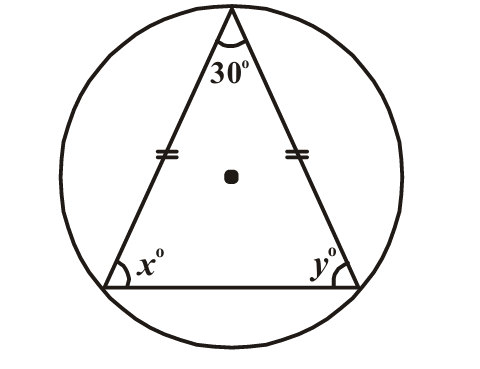
Solution:
From the figure, we can see angles 30°, x°, and y°.
Since the triangle is inscribed in a circle, we use the property that angles in the same segment are
The angle at the circumference is
Using the inscribed angle theorem and triangle angle sum:
Sum of angles in triangle =
30° + x° + y° = 180°
If the triangle appears to be isosceles from the figure:
x = y = (180° - 30°)/2 =
Therefore: x =
(ii)
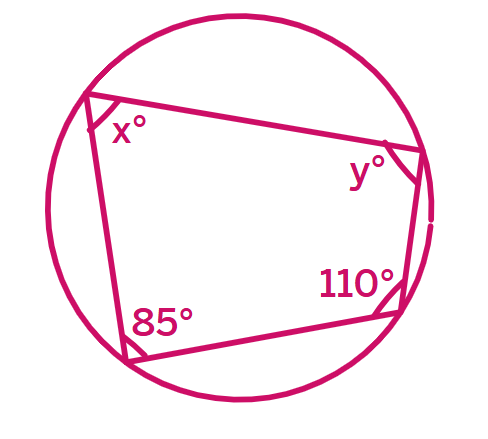
Solution:
From the figure: angles shown are 85°, x°, and 110°.
In a cyclic quadrilateral, opposite angles are
Therefore: 85° + 110° =
Wait, let me reconsider. If 85° and 110° are opposite angles:
This is impossible since 85° + 110° = 195° ≠ 180°
So 85° and x° must be opposite angles:
85° + x° =
x° = 180° - 85° =
(iii)
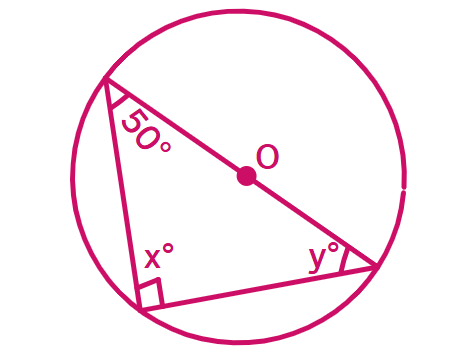
Solution:
From the figure: angle 50° and angles x°, y°.
If 50° is an inscribed angle and x° is the
Central angle =
x° = 2 × 50° =
For angle y°, using the triangle formed:
y° appears to be an inscribed angle equal to 50°
Therefore: y =
2. Given that the vertices A, B, C of a quadrilateral ABCD lie on a circle. Also ∠A + ∠C = 180°, then prove that the vertex D also lie on the same circle.
Solution:
Given: A, B, C lie on a circle and ∠A + ∠C =
To prove: D also lies on the same circle
Proof:
Since A, B, C lie on a circle, let's call this circle with center O.
We need to prove that D also lies on this circle.
Method: Proof by contradiction
Assume D does not lie on the circle through A, B, C.
Case 1: D lies inside the circle
Then ∠A + ∠C would be
Case 2: D lies outside the circle
Then ∠A + ∠C would be
But we are given that ∠A + ∠C =
This contradicts both cases above.
Therefore, D must lie
Hence, ABCD is a
Hence proved.
3. If a parallelogram is cyclic, then prove that it is a rectangle.
Solution:
Given: ABCD is a
To prove: ABCD is a
Proof:
Since ABCD is a parallelogram:
Opposite angles are
So: ∠A = ∠C and ∠B = ∠D
Since ABCD is cyclic:
Opposite angles are
So: ∠A + ∠C =
From ∠A = ∠C and ∠A + ∠C = 180°:
∠A + ∠A = 180°
2∠A =
∠A =
Therefore: ∠C =
Similarly: ∠B = ∠D =
Since all angles are 90°, ABCD is a
Hence proved.
4. Prove that a cyclic rhombus is a square.
Solution:
Given: ABCD is a
To prove: ABCD is a
Proof:
Since ABCD is a rhombus:
All sides are
Since ABCD is cyclic:
Opposite angles are
In a rhombus, opposite angles are
Let ∠A = ∠C = α and ∠B = ∠D = β
From cyclic property: ∠A + ∠C = 180°
α + α =
2α = 180°
α =
Therefore: ∠A = ∠C =
Similarly: ∠B = ∠D =
A rhombus with all angles equal to 90° is a
Hence proved.
5. For each of the following, draw a circle and inscribe the figure given. If a polygon of the given type can't be inscribed, write not possible.
(a) Rectangle
Solution:
Construction steps:
1. Draw a circle with center O
2. Draw a
3. Draw another diameter CD
4. Join AC, CB, BD, DA
5. ACBD is a
Reason: All angles subtended by a diameter are
(b) Trapezium
Solution:
Reason: In a cyclic quadrilateral, opposite angles sum to
In a general trapezium, this condition is not satisfied.
Exception: An
(c) Obtuse triangle
Solution:
Construction steps:
1. Draw a circle with center O
2. Mark any three points A, B, C on the circle
3. Ensure that one arc is
4. The angle opposite to the major arc will be
5. Join AB, BC, CA to form an obtuse triangle
(d) Non-rectangular parallelogram
Solution:
Reason: We proved in question 3 that any cyclic parallelogram must be a
Therefore, a non-rectangular parallelogram cannot be inscribed in a circle.
(e) Acute isosceles triangle
Solution:
Construction steps:
1. Draw a circle with center O
2. Mark point A on the circle
3. Mark points B and C
4. Ensure all arcs are
5. Join AB, BC, CA to form an acute isosceles triangle
(f) A quadrilateral PQRS with PR as diameter
Solution:
Construction steps:
1. Draw a circle with center O
2. Draw diameter
3. Mark any two points Q and S on the circle
4. Join PQ, QR, RS, SP
5. PQRS is the required quadrilateral
Property: ∠PQR = ∠PSR =
