Right-Angled Triangles and Pythagoras Property
Pythagoras, the Greek philosopher, in sixth century B.C. found a very important and useful property of right-angled triangles, thus giving birth to the famous namesake property.
This property was known to people of many other countries too. The Indian mathematician Baudhayan also gave an equivalent form for this property.
We now try to explain the Pythagoras property.
In a right-angled triangle, the sides have some special names.
The side opposite to the right angle is called the hypotenuse while the other two sides are known as the legs of the right-angled triangle.
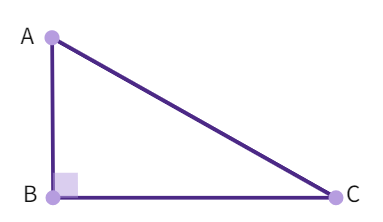
In ∆ABC, the right-angle is at
So, AC is the
AB and BC are the legs of ∆ABC. 'a' , 'b' and 'c' are sides opposite to angles ∠A , ∠B, ∠C respectively, using convention.
Proof
Have a look at the figure on the right. The square has side length
Now let’s rearrange the triangles in the square. The result still contains the four right-angles triangles, as well as two squares of size
So total uncovered region area is
Comparing the area of the red area and the rearrangement, we see that
This is the original proof that
This is Pythagoras property. It may be stated as follows.
Mathematical Interpretation: In a right-angled triangle, the square on the hypotenuse = sum of the squares on the legs.
It says that for any right-angled triangle, the square of the length on the hypotenuse is equal to the sum of the squares of the lengths on the legs.
If you have a right-angled triangle, the Pythagoras property holds. But is the reverse true? That is, If the Pythagoras property holds for some triangle, will the triangle be right-angled?.
As it turns out, the converse is also true.
This shows that Pythagoras property holds if and only if the triangle is right-angled.
Hence we get another property:
If the Pythagoras property holds, the triangle must be right-angled.
The diagonal of a rectangle produce by itself the same area as produced by its length and breadth’– This is Baudhayan Theorem. Compare it with the Pythagoras property.
Baudhayan Theorem is defined with respect to a rectangle.
It contains a list of Pythagorean triples discovered algebraically, a statement of the Pythagorean theorem, and a geometrical proof of the Pythagorean theorem for an isosceles right triangle.
Phythagoras theorem can be proved for any type of triangle.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
Solution:
We see that: 9 + 16 =
So,
Therefore, the triangle is right-angled.
Note: In any right-angled triangle, the hypotenuse happens to be the longest side. In this example, the side with length 5 cm is the hypotenuse.
∆ ABC is right-angled at C. If AC = 5 cm and BC = 12 cm find the length of AB.
Fig
Solution:
A rough figure will help us Fig.
By Pythagoras property,
=
(or)
So, AB =
Thus, the length of AB is 13 cm.
Note: To identify perfect squares, you may use prime factorisation technique.
1. Find the unknown length x in the following figures:
a
Solution:
As we know in a Right-angled Triangle: By Pythagoras Theorem,
So, using this theorem,
(i)
Thus, x =
Therefore, the value of x is 5.
b
Solution:
As we know in a Right-angled Triangle: By Pythagoras Theorem,
So, using this theorem,
(ii)
Thus, x = 10
c
Solution:
As we know in a Right-angled Triangle: By Pythagoras Theorem,
So, using this theorem,
(iii)
Thus, x = 17
d
Solution:
As we know in a Right-angled Triangle: By Pythagoras Theorem,
So, using this theorem,
(iv)
Thus, x = 25
e
Solution:
(v) In this question as we can see from the figure, it is making the right angle with the half-length of x, so
x = 2 ×
Thus, x = 70
f
Solution:
As we know in a Right-angled Triangle: By Pythagoras Theorem,
So, using this theorem,
(vi)
Thus, x = 13
Baudhayan Theorem
Baudhayan, an ancient Indian mathematician, stated that:
In a right-angled triangle, the square of the length of the hypotenuse (diagonal of a rectangle) is equal to the sum of the squares of the lengths of the other two sides (length and breadth).
This can be mathematically expressed as:
where: d is the diagonal (hypotenuse), l is the length, b is the breadth.
In Baudhayan's version, the focus is on the diagonal of a rectangle, which can be extended to the hypotenuse of a right-angled triangle.
Baudhayan's theorem predates Pythagoras and provides an early recorded instance of the mathematical concept later attributed to Pythagoras. This demonstrates that the understanding of this relationship between the sides of right-angled triangles was known in ancient India before it was formalized in Greece.
Pythagoras Theorem
Pythagorean Theorem, named after the Greek mathematician Pythagoras, states that:
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
This is expressed as:
where: c is the hypotenuse, a and b are the other two sides of the triangle.
Pythagoras's version is typically presented within the context of a right-angled triangle directly.
Note: (1) Both the Baudhayan Theorem and the Pythagorean Theorem state the same fundamental property of right-angled triangles.
(2) Both recognize that the area formed by squaring the hypotenuse (or diagonal in the context of the rectangle) is equal to the combined areas formed by squaring the other two sides.
Enrichment activity
There are many proofs for Pythagoras theorem, using ‘dissection’ and ‘rearrangement’procedure. Try to collect a few of them and draw charts explaining them.
Solution:
Pythagoras' Theorem, which states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides
(
1.Bhaskara's Proof
2.Euclid's Proof
3.Garfield's Proof
