Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 9: Perimeter and Area

    Introduction

    Area of a Parallelogram

    Area of a Triangle

    Circles

    Area of Circle

    Exercise 9.1

    Exercise 9.2

    What Have We Discussed ?

    Extra Curriculum Support

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 9: Perimeter and Area > Area of a Triangle

Area of a Triangle

Let us find a method to get the area of a triangle with an activity.

Activity: There are two copies of a triangle. Rotate the second triangle and place it such that the pair of corresponding sides are joined. Once you think they are joined properly drag and select both the triangles. The system will identify if you have placed it correctly or not.

${message}

The figure that we obtain is a .

The area of the parallelogram will be the sum of the area of the two triangles, in other words - twice the area of the random triangle that we have cut out. Also, we observe that the base and the height of the triangle is equal to the base and the height of the parallelogram. Therefore,

Area of each triangle = \frac{1}{2} (Area of parallelogram) = \frac{1}{2} (base × height)

= \frac{1}{2} b × h

Similarly, make random parallelograms on paper and cut them along the diagonal, so that two triangles are formed. Draw a line from C to B to cut it into two triangles.

Move the triangles around and see if they are congruent. Are the triangles obtained congruent?

1. Try the above activity with different types of triangles.

Lets draw different triangles and explore more. In the below canvas, draw line from A to X,Y,C and from B to X,Y,C.

In the above figure, the threr triangles (∆ABC, ∆ABY and ∆) are on the same base and have a common height.

Can we say all the triangles are equal in area? .

Are the triangles congruent also? .

All the congruent triangles are equal in area but the triangles equal in area need not be congruent

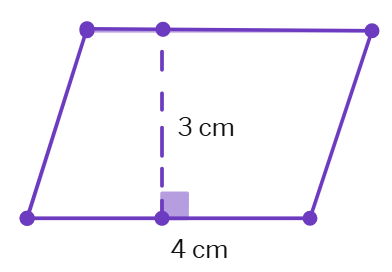
One of the sides and the corresponding height of a parallelogram are 4 cm and 3 cm respectively. The area of the parallelogram (cm2)

Instruction

Area of the parallelogram = cm2
Area of the parallelogram = base × height = 4 cm × cm = cm2

What is the value of height ‘x’, if the area of the parallelogram is 24 cm2 and the base is 4 cm.

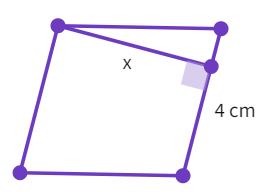
Finding the height of the parallelogram

  • We know that area of parallelogram is
  • Putting the given values in the equation
  • Solving to find the height which is cm
  • Simplifying
  • We have found the height

The two sides of the parallelogram ABCD are 6 cm and 4 cm. The height corresponding to the base CD is 3 cm. Find the:

(i) area of the parallelogram

(ii) the height corresponding to the base AD

Area of paralleogram =

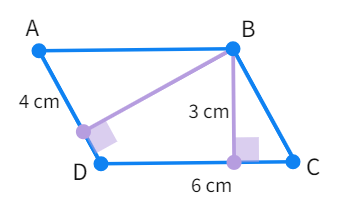
  • Area of parallelogram = cm2
  • Let the height corresponding to base AD be h . We also know that AD = cm
  • We can write cm2 =
  • Simplifying
  • Calculating we get h = cm
  • Finding the value of h i.e. required height.

Find the area of the following triangles Fig.

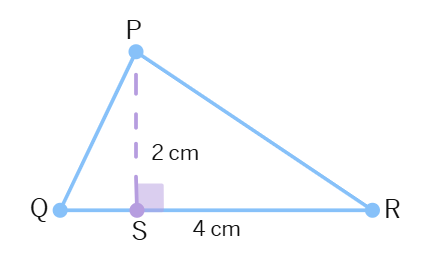
(i)

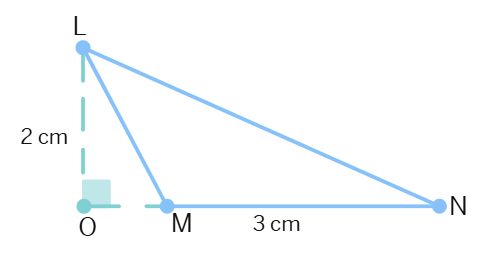
(ii)

(i)Area of triangle = 12bh = 12 × QR × PS
= 12 × × = cm2
(ii)Area of triangle = 12bh = 12 × ×
= 12 × 3 × 2 = cm2

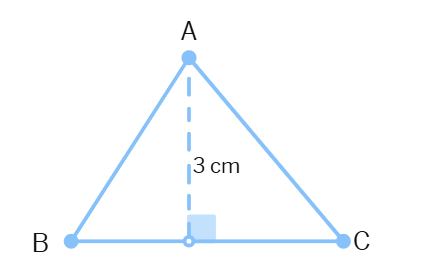
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm Fig.

Height = cm, Area = cm2

Area of the triangle ABC = 12bh

(or) 36 = 12 × b × 3 i.e., b = 36×23 = cm

So, BC = cm.

In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm (Check the below figure).

Find:

(i) the area of the ∆PQR

(ii) QM

Finding area of PQR

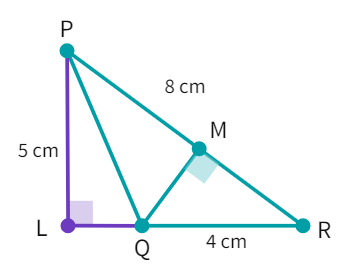
  • From the fig., we can see that ∆PQR has base = cm and height = cm
  • Thus, the area is equal to cm2
  • We can use this area for finding QM (h) i.e the height and we already know that PR= cm
  • Putting the values in the equation: cm2 =
  • Simplifying
  • Calculating
  • We get QM = cm
  • QM value is found