Extra Curriculum Support
Enhanced Curriculum Support
This is a comprehensive educational resource designed to provide students with the tools and guidance necessary to excel. This support system is structured to cater to various aspects of learning, ensuring that students are well-prepared for academic challenges and practical applications of mathematical concepts. Some are the key benefits are mentioned below:
1.Comprehensive Learning: This holistic approach helps students gain a thorough understanding of the subject. Practical Application: The resources encourage students to apply mathematical concepts to real-life scenarios, enhancing their practical understanding and problem-solving skills.
2.Critical Thinking and Reasoning: Value-Based and HOTS questions promote critical thinking and reasoning abilities. These skills are crucial for students to tackle complex problems and make informed decisions.
3.Exam Preparedness: Sample Question Papers and NCERT Exemplar Solutions provide ample practice for exams. They help students familiarize themselves with the exam format and types of questions, reducing exam anxiety.
4.Ethical and Moral Development: Value-Based Questions integrate ethical and moral lessons into the learning process, helping in the overall development of students' character and social responsibility. By incorporating these diverse elements, Enhanced Curriculum Support aims to provide a robust and well-rounded knowledge, preparing students for both academic success and real-world challenges.
Sec A
1. A ? connects a vertex of a triangle to the mid-point of the opposite side.
A. altitude B. median C. angle bisector D. perpendicular bisector
Sec B
1. Find the circumference of the circles with the radius of 30mm.
2. Find the circumference of the inner and the outer circles with a radius of 5 and 15.
Sec C
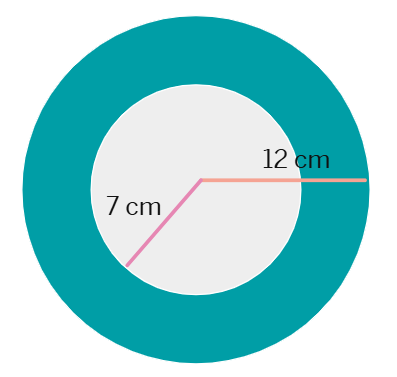
1. In the figure given below, a circle is inscribed inside another circle. The radius of the outer circle is 12 cm and that of the inner circle is 7 cm. Find the area of the shaded portion between the circles.
2. The radius of a circular pipe is 25 cm. What length of a tape is required to wrap once around the cylinder?
Sec D
1. The perimeter of a square is same as that of the rectangle. Find the side of the square if the dimensions of the rectangle are 10 m × 8 m.
2. Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Value-Based Questions
Problem 1
Question: Ria and her friends are planning to plant trees in a park. The park is in the shape of a rectangle with a length of 60 meters and a width of 40 meters. They decided to plant trees around the boundary of the park. Calculate the perimeter of the park and discuss how planting trees around the boundary helps in environmental conservation and community well-being.
Problem 2
A farmer wants to fence his rectangular field, which has a length of 150 meters and a width of 80 meters. He also wants to divide the field into two equal parts using a fence parallel to its width. Find the total length of the fence required. Why is it important for farmers to measure the perimeter of their fields accurately when planning such activities?
HOTS
Q1
A rectangular garden has a length that is twice its width. If the perimeter of the garden is 96 meters, find the dimensions of the garden. Additionally, if the garden is to be paved with tiles that each cover an area of 1 square meter, determine how many tiles are needed. Explain the process of how you arrived at your answer and the importance of understanding the relationship between perimeter and area in real-life scenarios like landscaping.
Q2
A playground is designed in the shape of a trapezium with parallel sides measuring 80 meters and 120 meters, and the distance between these parallel sides is 50 meters. Calculate the area of the playground. If the playground is to be divided into smaller sections for different activities and each section has to be of equal area, how would you determine the number of sections? Discuss how knowing the area helps in planning and optimizing space usage in community projects.
Q3
A circular track has a radius of 30 meters. If a runner completes 4 laps around the track, calculate the total distance covered by the runner. Compare this with the area of a square field with a side length equal to the diameter of the track. Which is larger, and by how much? Discuss the practical implications of understanding the concepts of perimeter and area when comparing different shapes and planning activities that involve space and distance.
NCERT Exemplar Solutions
Questions
1. Area of a right triangle is 54
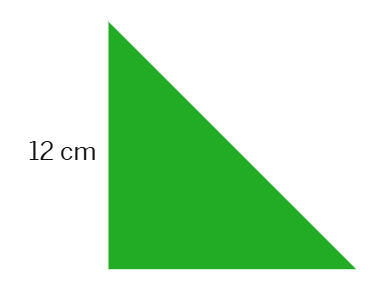
(a) 18 cm (b) 27 cm (c) 36 cm (d) 54 cm
2. ? squares of each side 1 m makes a square of side 5 km.
3. All the triangles equal in area are congruent.
4. Ratio of the circumference and the diameter of a circle is more than 3.
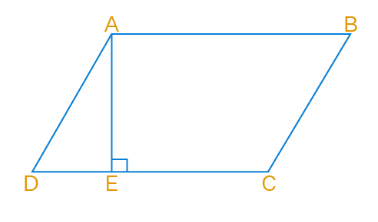
5. In Fig ABCD is a parallelogram, in which AB = 8 cm, AD = 6 cm and altitude AE = 4 cm. Find the altitude corresponding to side AD.
6. Circumference of a circle is 33 cm. Find its area.
7. Circumference of a circle is always
(a) more than three times of its diameter
(b) three times of its diameter
(c) less than three times of its diameter
(d) three times of its radius
8. All congruent triangles are equal in area.
9. Ratio of circumference of a circle to its radius is always 2π : I.
10. A hedge boundary needs to be planted around a rectangular lawn of size 72 m × 18 m. If 3 shrubs can be planted in a metre of hedge, how many shrubs will be planted in all?
11. Area of an isosceles triangle is 48
12. The dimensions of a plot are 200 m × 150 m. A builder builds 3 roads which are 3 m wide along the length on either side and one in the middle. On either side of the middle road he builds houses to sell. How much area did he get for building the houses?
13. A room is 4.5 m long and 4 m wide. The floor of the room is to be covered with tiles of size 15 cm by 10 cm. Find the cost of covering the floor with tiles at the rate of ₹ 4.50 per tile.
14. A circular pond is surrounded by a 2 m wide circular path. If outer circumference of circular path is 44 m, find the inner circumference of the circular path. Also find area of the path.
15. A school playground is divided by a 2 m wide path which is parallel to the width of the playground, and a 3 m wide path which is parallel to the length of the ground. If the length and width of the playground are 120 m and 80 m respectively, find the area of the remaining playground.
16. Ramesh grew wheat in a rectangular field that measured 32 metres long and 26 metres wide. This year he increased the area for wheat by increasing the length but not the width. He increased the area of the wheat field by 650 square metres. What is the length of the expanded wheat field?
17. 4 squares each of side 10 cm have been cut from each corner of a rectangular sheet of paper of size 100 cm × 80 cm. From the remaining piece of paper, an isosceles right triangle is removed whose equal sides are each of 10 cm length. Find the area of the remaining part of the paper.
Case-Based Questions
Q1
Case: Garden Design
Scenario: Anitha wants to design a new garden in her backyard. She has a rectangular area that she wants to divide into three different sections for flowers, vegetables, and a small sitting area. The total length of the rectangular garden is 12 meters and its width is 8 meters.
Questions:
1. Calculate the total area of the garden.
2. If Anitha wants to allocate half of the garden's area for flowers, one-third for vegetables, and the rest for the sitting area, how much area will each section have?
3. Explain how Anitha should plan the garden layout based on the area of each section to ensure she uses the space efficiently.
Q2
Case: Park Planning
Scenario: A city park is designed with a rectangular walking path and a central playground. The walking path surrounds a central rectangular playground. The total perimeter of the park (including the walking path) is 400 meters, and the width of the walking path is 4 meters. The length of the playground is twice its width.
Questions:
1. Determine the dimensions of the playground.
2. Calculate the area of the walking path.
3. Discuss how understanding the area of both the playground and the walking path can help in planning the park's usage and ensuring that the walking path is of sufficient size for the number of park visitors.
