Exercise 9.2
Find the circumference of the circles with the following radius:(Take π =
Hint: Cicrcumference of the circle = 2πr
Solution:
(a)14 cm
Substitute a value in r = 2 ×
= 2 ×
(b)28 cm
Substitute b value in r = 2 ×
= 2 ×
(c)21 cm
Substitute c value in r = 2 ×
= 2 ×
Find the area of the following circles.
Hint: We know that the Area A of a circle of radius r is given by A = π
(a) radius = 14 mm (Take π =
(b) diameter = 49 m
(c) radius = 5 cm
3. If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. (Take π =
- Since, we know the circumference, we can find the radius using the formula: circumference =
- Putting the values,
= r ,where r is the radius. - Thus, r =
m - Now, using this value to get the area of the sheet.
- Area of sheet =
m 2 - Thus, we have found the required values.
4. Say, we have a field similar to the area in the previous question. Now, a gardener wants to fence the shaded region (as in the previous figure). What is the length and cost of the rope needed for fencing?
Additional Information:
Rope needs to make 2 rounds of fence
Cost = Rs 4 per meter and π =
Note: Take the numerical values from previous question but in meters.
- Fro calculation of rope length, we need to find the
of the field. - The total perimeter will be
of the two perimeters. - Perimeter of larger circle =
π - Perimeter of smaller circle =
π - Total Perimeter = 28π =
m. - Since, we need to make 2 rounds of the fence, the length of rope required is
m. - Since, the cost of the rope per m is Rs.4, the cost of the rope is Rs.
- Cost of the rope is Rs.704
From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Radius of circular sheet(r1) =
Radius of removed circle(r2) =
Area of remaining sheet = Area of circular sheet - Area of removed circle - π
= π(
=
= 3.14(16 - 9)
Thus, the area of the remanining sheet is 21.98
6. Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs Rs.15
(Take π = 3.14)
- Since, we know the diameter, we can find the circumference as cicumference =
where d is the diameter. - Thus, circumference of table =
m - Since, the lace cost is Rs.15 per m, the cost of the lace required is Rs.
- Thus, we have found the cost to be Rs. 70.65
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
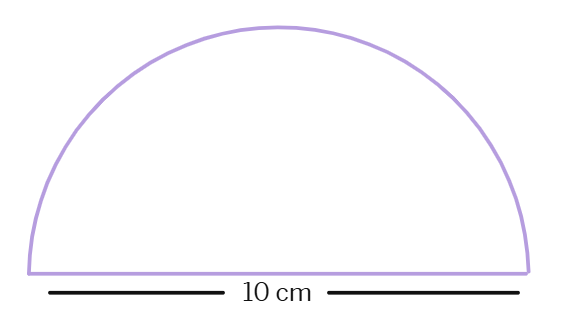
Thus, the perimeter of the given figure is 25.71 cm
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15/
Diameter of the circular tabletop =
Radius of the circular tabletop =
Area of circular tabletop =
= 3.14 ×
Since, the cost of 1
The cost of polishing 2.0096
Thus,the cost of the polishing a circular tabletop is ₹ 30.144.
9. Shazli took a wire of length 44 cm and bent it into the shape of a circle.
(a) Find the radius of the circle
(b) Find the area of the circle
(c) If the same wire is bent into the shape of a square, find the length of each of side.
(d) Which figure encloses more area, the circle or the square?
(Take π =
- We have the
of the circle as 44 cm. - Using the circumference formula to find the radius
- Thus, the radius is found to be
cm - Finding the area of the circle, we get
cm 2 - Taking the same wire, we make a square.
- The length of the side for this square is
cm - Thus, the area of the square is
cm 2 - On comparison, the
has the larger area.
10. Sarita wants to make a mask and uses a circular card sheet of radius 14 cm. For provision of sight and speech respectively, she makes two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1cm and cuts them off. Find the area of the mask.
(Take π = )

- The area of the circular sheet =
cm 2 - Now, finding area of the two smaller circles
- Total area of the two small circles is
cm 2 - Finding the area of the rectangular mouth, we get
cm 2 - Thus, calculating the area of the mask
cm 2 - The area of the mask is found to be 536
cm 2
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Solution:
Square piece of aluminum sheet =
Radius of circle =
Area of aluminium sheet left = Total area of square aluminium sheet - Area of circle
= side × side - π
= 6 ×
Therefore, the area of the aluminum sheet left is 23.44
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle? (Take π = 3.14)
Circumference of the circle =
Radius of the circle = 2πr =
2 ×
r =
Area of the circle = π
= 3.14 ×
Therefore, the radius and area of the circle are 5 cm and 78.5
13. A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (Round off to one decimal place and π = 3.14)
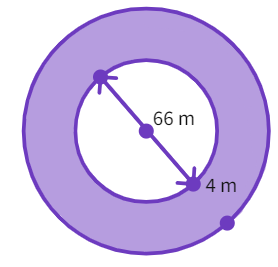
- Radius of flower bed =
m - Now, Area of flower bed =
m 2 - The radius of the flower bed and path together is
m - Finding the area of the flower bed and path, we get
m 2 - Thus, calculating the area of the path
m 2 - The area of the path is found to be 879.2
m 2
14. A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden?
(Take π = 3.14)
- To check we need to calculate the
of the circular garden - Knowing the garden area, we find that the radius is
m. - Since, the sprinker can cover a radius of 12m, it
water the garden. - Thus, the garden can be watered by the sprinkler
15. How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π = )
- To check rotations, we need to calculate the
of the wheel. - Substituting
- Calculating we get
cm - Wheel circumference = 176 cm
- To calculate the rotations
- We can write:
= x n (n - number of rotations) - Substituting
- Thus, n(number of rotations) =
- Substituting
- Thus, the number of rotations to cover the given distance is equal to 200.
How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π =
Radius =
Circumference of wheel = 2πr
= 2 ×
= 2 ×
Total distance = 352m =
Number of times the wheel should rotate =
=
17. The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour. (Take π = 3.14)
- For distance covered, we need to calculate the
of the cicular path made by the clock hand. - Substituting
- Calculating we get
cm - Circumference for one rotation = 94.2 cm
- Number of rotations made by the minute hand is one hour =
- Substituting
- Thus, distance covered by minute hand in one hour is 94.2 cm.
