Exercise 9.1
1. Find the area of each of the following parallelograms.
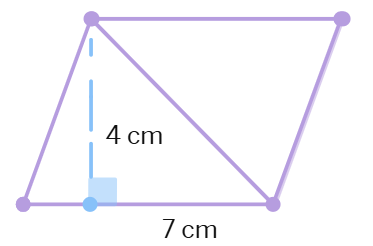
(a)
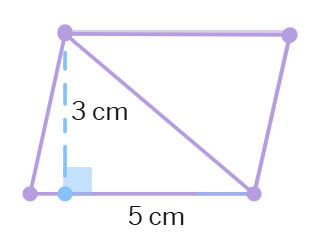
(b)
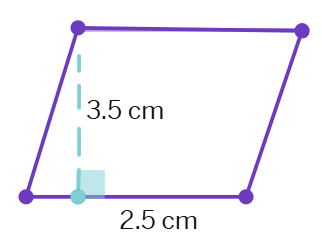
(c)
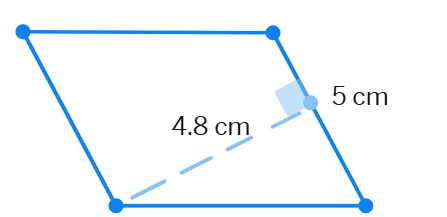
(d)
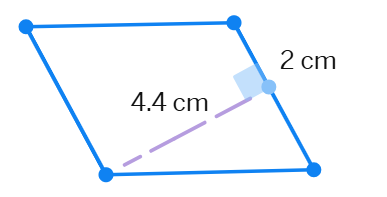
(e)
Find the area of each of the following triangles.
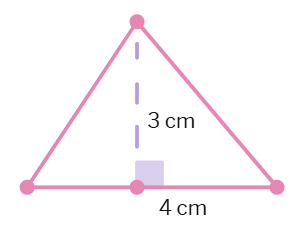
(a)
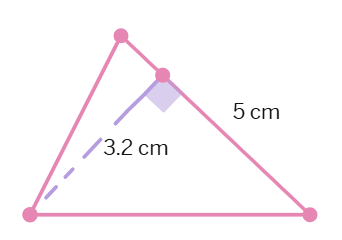
(b)
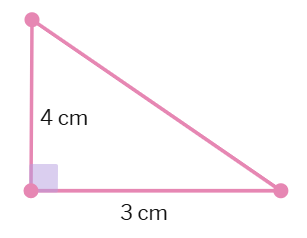
(c)
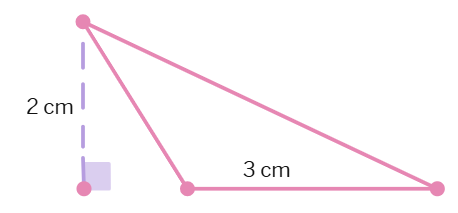
(d)
- Fill in the blanks for the given area of parallelograms
| S.No | Base | Height | Area of Parallelograms |
|---|---|---|---|
| (a) | 20 cm | 246 | |
| (b) | 15 cm | 154.5 | |
| (c) | 8.4 cm | 48.72 | |
| (d) | 15.6 cm | 16.38 |
Solution: Using the area of parallelogram formula: Area of parallelogram = base × height
(a) Height =
(b) Base =
(c) Base =
(d) Height =
- Fill in the blanks for the given area of triangles
| S.No | Base | Height | Area of Triangle |
|---|---|---|---|
| (a) | 15 cm | 87 | |
| (b) | 31.4 mm | 1256 | |
| (c) | 22 cm | 170.5 |
Solution: Using the area of triangle formula: Area of triangle =
(a) Height =
(b) Base =
(c) Height =
PQRS is a parallelogram Fig. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm.
Find: (a) the area of the parallegram PQRS
(b) QN, if PS = 8 cm
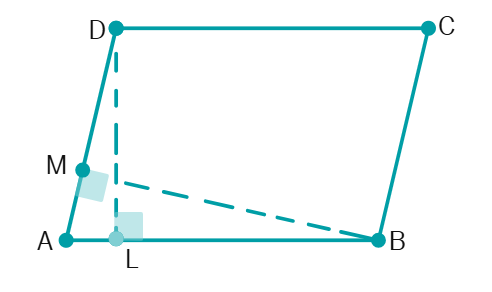
In parallelogram ABCD, DL and BM are the heights on the sides AB and AD, respectively. If the area of the parallelogram is 1470
- From the fig., we know that parallelogram has area =
cm 2 - To find BM, we need to take
as base which has a value of cm - We can write:
cm 2 where BM = h - We get, BM = h =
cm - Similarly, to find DL we take
as base which has a value of cm - We can write:
cm 2 where DL = y - We get DL = y =
cm - BM and DL values have been found
∆ABC is right angled at A (shown below). AD is perpendicular to the side BC. If the length of the sides are: AB = 5 cm, BC = 13 cm and AC = 12 cm, find the area of ∆ABC. Also find the length of AD
- From the figure, we can see that the sides:
acts as height and acts as base for the triangle (both are interchangeable) - Thus, the area is equal to
cm 2 - Using this area to find, AD where we have
acting as base. cm 2 where length of AD is s. - Simplifying
- Calculating i.e. s =
cm - Value of height AD
∆ABC is an isosceles triangle with AB = AC = 7.5 cm and BC = 9 cm. The height AD, from A to BC is 6 cm. What is the area of ∆ABC. Also find the height from C to AB i.e. CE?
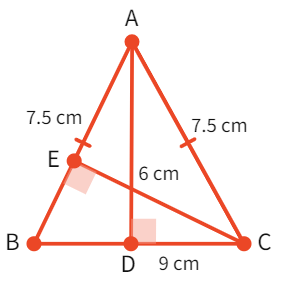
- From the figure, we can see that the area of the traingle can be sound using
as height and as base. - Thus, the area is equal to
cm 2 - Using this area to find CE where we have
acting as base (equal to cm). cm 2 where length of CE is h. - Simplifying
- Calculating i.e. h =
cm - Value of height CE
