Area of Circle

In the earlier section, we spoke about putting ribbons along the border of circular cardboard cutouts. Say, we need to colour the cutouts using crayons. How many crayons will be required?

How much time will it take to do this task?

This is all concerned with the amount of area that needs to be coloured.

In other real-life scenarios:

• Say, a gardener needs to fertilise a circular flower bed of radius 7 m. If 1 kg of fertiliser is required for 1 square metre area, how much fertiliser he needs to purchase?

• We need to polish a circular table-top of radius 2 m, with the cost of polishing being Rs. 10 per square metre. How much money do we need to get the work done?

To find the area of a circle, let us do an activity.

Activity: Draw a circle and shade one half of the circle with any colour. Now fold the circle and divide the circle into a total of eight parts. Once this is done, cut along the folds.

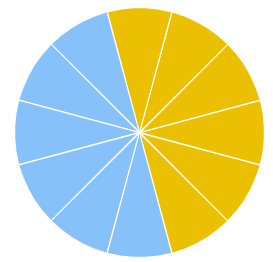
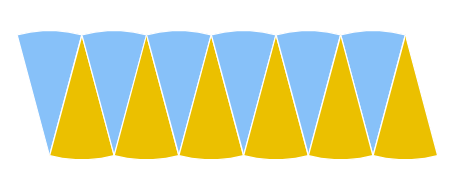
Now, arrange the eight separate sections as shown above. We see that the sections together form (roughly) a .

As the more sectors that we make increases, the nearer we reach to an appropriate rectangle (which is, as we know, a type of parallelogram), upon arranging the sections together in a straight line.

Now, what can be said about the breadth of this rectangle that is being formed?

From the figures, we can deduce that the breadth of the rectangle is equal to the radius(r)diameter(2r) of the circle.

Say, we divide the entire circle into 64 equal sectors. On doing so, we will get, on each side, 32 sectors. Thus, the length of the formed rectangle is equal to the length of the 32 sectors i.e. the length is 121314 of the circumference of the circle.

Draw circles of different radii on a graph paper. Find the area by counting the number of squares. Also find the area by using the formula. Compare the two answers.

By using graph paper,we find that their respective areas are 4 cm2 and 12cm2 respectively.

By using the formula,we find that their respective areas are ((227 × 1)) cm2 = cm2

((227 × 4)) cm2 = / cm2

= cm2

Thus, we see that the two values differ.

Find the area of a circle of radius 30 cm (use π = 3.14).

Solution:

Radius, r = cm

Area of the circle = πr2 = 3.14 × 302 = cm2.

Diameter of a circular garden is 9.8 m. Find its area.

Solution:

Diameter, d = 9.8 m.

Therefore, radius r = 9.8 ÷ 2 = m

Area of the circle = πr2 = 227 × 4.92 m2

= cm2

The adjoining figure shows two circles with the same centre (a) The radius of the larger circle = 10 cm , (b) The radius of the smaller circle = 4 cm , (c)π = 3.14

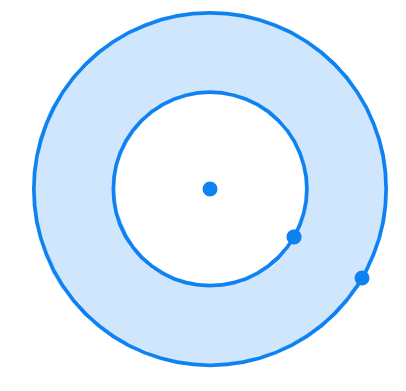
Find: (assume value of π to be 3.14)

(a) the area of the larger circle

(b) the area of the smaller circle

(c) the shaded area between the two circles

Instruction