Geometric Verification of the Identities
Let me explain each geometric proof:
The total square has sides of length (a+b)
It's divided into four regions:
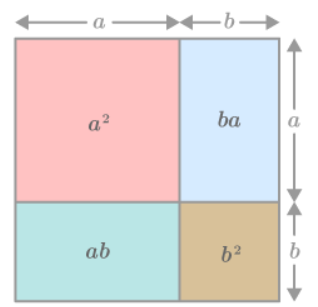
Top left: a × a =
Top right: a × b =
Bottom left: b × a =
Bottom right: b × b =
Adding these areas:
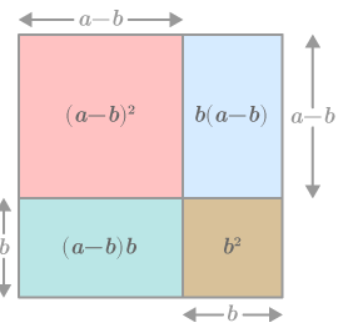
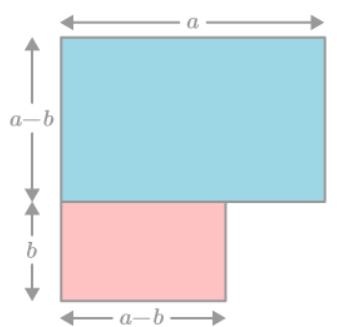
Divide both the rectangles horizontally and vertically by drawing a straight line such that the length and width of two shapes are equal to 'b' then the length and width of the remaining two shapes are equal to '(a-b)'.
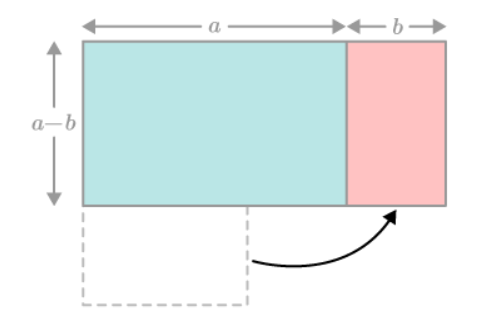
Now, calculate the area of each geometrical shape mathematically.
The final result is
(a+b)(a-b) Proof
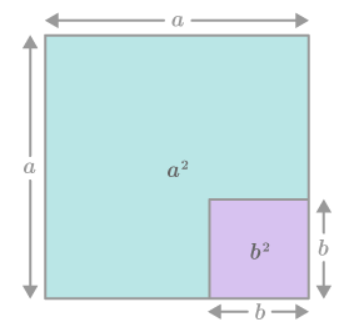
Begin with a square of side length a with area =
Subtract a square of area
The remaining area represents
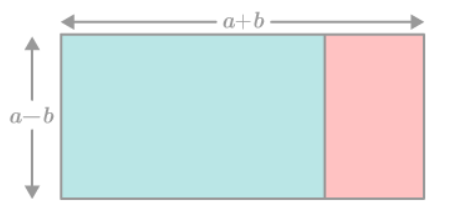
The dimensions of the resulting rectangle are (a+b) and (a-b).