Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 9: Area of Plane Figures

    Introduction

    Area of a Trapezium

    Area of a Quadrilateral

    Area of a Rhombus

    Surveying the Field

    Area of a Polygon

    Area of a Circle

    Area of a Circular Path or Area of a Ring

    Length of the Arc

    Area of Sector

    Exercise 9.1

    Exercise 9.2

    What We Have Discussed?

    Easy Level Worksheet

    Moderate Level Worksheet

    Hard Level Worksheet

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 9: Area of Plane Figures > Area of a Polygon

Area of a Polygon

When trying to find area of a random polygon, logically, we can simply split the given polygon into smaller familiar geometric shapes and then proceed to find the areas of the individual pieces before adding them up.

Figure (a)

Figure (b)

Above in Figure (a), we can draw the diagonals AC and AD which leads to the polygon being split into three smaller and non-congruent triangles. We can draw their corresponding heights and proceed to calculate the individual areas and add them up

(OR)

we can follow Figure (b), drawing just one diagonal (AD) and getting one trapezium and a triangle. From here on, the process is the same.

Example 1: The area of a trapezium shaped field is 480 m2, the distance between two parallel sides is 15 m and one of the parallel side is 20 m. Find the other parallel side.

Instructions

Finding the second parallel side

  • We know that, the area of a trapezium: unit2 where h - height , a and b - the length of the parallel sides.
  • Substituting the values given to us in equation.
  • Length of the second parallel side: m
  • Thus, we have got the desired value.

Example 2: The area of a rhombus is 240 cm2 and one of the diagonals is 16 cm. Find the other diagonal.

Instructions

Let length of one diagonal d1 = cm and length of the other diagonal = d2
Area of the rhombus = 12× d1× d2 = 12× × d2 =
d2 = 240×216 = cm.
Hence, the length of the second diagonal is 30 cm.

(ii) Polygon ABCDE is divided into parts. Find its area if:

AD = 8 cm , AH = 6 cm , AG = 4 cm

AF = 3 cm , BF = 2 cm

BF = 2 cm , CH = 3 cm , EG = 2.5 cm

Polygon ABCDE

Instructions

Finding the area of the polygon

  • We can see from the above figure, that the polygon ABCDE has been divided into 3 and 1 .
  • The area of a triangle: where b - base length and h - height length
  • The area of a trapezium: where h - height , a and b - the length of the parallel sides.
  • Finding the individual areas: Area of ABF = cm2, Area of CHD = cm2
  • Area of ADE = cm2, Area of BCHF = cm2
  • Total area sum: cm2
  • We got the desired value.

(iii) Find the area of polygon MNOPQR, if MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm NA, OC, QD and RB are perpendiculars to diagonal MP.

Instructions

We have the following shapes: triangles and trapeziums.
For △MAN = 12 × × 2.5 = , △OCP = 12 × × 3 = , △QDP = 12 × × 2 = and △MBR = 12 × × 2.5 =
For trapezium(BCON) = 12 × (3+2.5) × = and trapezium(BRQD) 12× (2+2.5) × =
Thus, the total area becomes cm2.

Example 3: There is a regular hexagon ABCDEF of side 5 cm. Aman and Riddhima divided it in two different ways as indicated in below figures. Find the area using both methods.

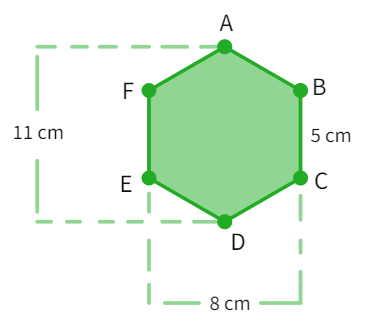
(a) Polygon ABCDEF

Aman's method

Instructions

Dividing the hexagon into two trapeziums

  • Upon using the above given dimensions: Height of each trapezium = cm
  • Substituting the value we get
  • Area of one trapezium: cm2
  • Area of polygon ABCDEF: cm2
  • We have found the area using Aman's method.

Riddhima's method

Instructions

Finding values of the two triangles, one rectangle

  • Upon using the above given dimensions: Height of each triangle = cm
  • Substituting the value we get
  • Area of each triangle: cm2, Area of rectangle: cm2
  • Area of polygon ABCDEF: cm2
  • We have found the area using Ridhima's method.