Exercise 9.1

2. Find the area enclosed by each of the following figures

(i).

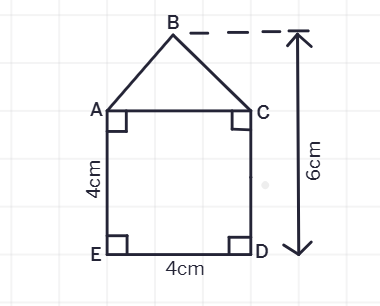
Solution:

The figure can be divided into two parts: a square and a triangle.

The side of the square is cm.

Area of the square = side × side

Area of the square = 4 cm × 4 cm

Area of the square = cm2

The base of the triangle is the same as the side of the square, which is 4 cm.

The height of the triangle is the difference between the total height and the side of the square: 6 cm - 4 cm = cm.

Area of the triangle = (12) × base × height

Area of the triangle = (12) × cm × cm

Area of the triangle = cm2

Total area = Area of the square + Area of the triangle

Total area = cm2 + cm2

Total area = cm2

Therefore, the total area enclosed by the figure is 20 cm2.

(ii).

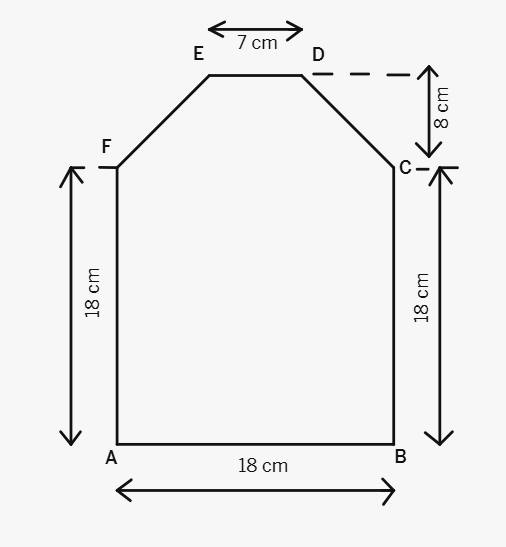
Solution:

The figure can be divided into three parts: a rectangle and two trapeziums.

Area of the rectangle = length × width

Area of the rectangle = cm × cm

Area of the rectangle = cm2

Area of one trapezium = (12) × (sum of parallel sides) × height

Parallel sides of the trapezium are 7 cm and 18 cm, and the height is 5 cm.

The height is found by subtracting the length of the rectangle from the total height.

18 cm + 8 cm = cm.

= cm - 18 cm = cm.

Then divide by 2 since there are two trapezoids, 8cm2 = 4cm.

However, the picture shows 8cm total height, so the height of the trapezoid is 8cm - 3cm = cm

Area of one trapezium = (12) × (7 cm + 18 cm) × 5cm.

Area of one trapezium = (12) × 25 cm × 5cm

Area of one trapezium = cm2

Since there are two trapeziums, the total area of the trapeziums is 2 × 62.5 cm2 = cm2

Total area of the figure = Area of the rectangle + Area of the two trapeziums

Total area of the figure = 324 cm2 + 125 cm2

Total area of the figure = cm2

Therefore, the total area enclosed by the figure is 449 cm2.

(iii).

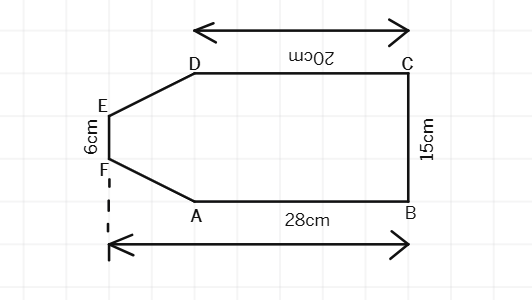
Solution:

The figure can be divided into three parts: a rectangle and two trapeziums.

Area of the rectangle = length × width

Area of the rectangle = cm × cm

Area of the rectangle = cm2

Area of one trapezium = (12) × (sum of parallel sides) × height

Parallel sides of the trapezium are 6 cm and 20 cm, and the height is (28cm - 20cm)2 = 8cm2 =

Area of one trapezium = (12) × (6 cm + 20 cm) × 4 cm

Area of one trapezium = (12) × cm × cm

= cm2

Since there are two trapeziums, the total area of the trapeziums is 2 × 52 cm2 = cm2

Total area of the figure = Area of the rectangle + Area of the two trapeziums

Total area of the figure = 300 cm2 + 84 cm2

Total area of the figure = cm2

Therefore, the total area enclosed by the figure is 384 cm2.

3. Calculate the area of a quadrilateral ABCD when length of the diagonal AC = 10 cm and the lengths of perpendiculars from B and D on AC be 5 cm and 6 cm respectively.

Solution:

Given: Diagonal AC = cm

Perpendicular from B to AC = cm

Perpendicular from D to AC = cm

The area of quadrilateral ABCD can be calculated as the sum of the areas of two triangles, ABC and ADC.

Area of triangle ABC = (12) × base × height

Area of triangle ABC = (12) × AC × perpendicular from B

Area of triangle ABC = (12) × cm × cm

Area of triangle ABC = cm2

Area of triangle ADC = (12) × base × height

Area of triangle ADC = (12) × AC × perpendicular from D

Area of triangle ADC = (12) × cm × cm

Area of triangle ADC = cm2

Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ADC

Area of quadrilateral ABCD = cm2 + cm2

Area of quadrilateral ABCD = cm2

Therefore, the area of quadrilateral ABCD is 55 cm2.

4. Diagram of the adjacent picture frame has outer dimensions 28 cm × 24 cm and inner dimensions 20 cm × 16 cm. Find the area of the shaded part of the frame, if the width of each section is the same.

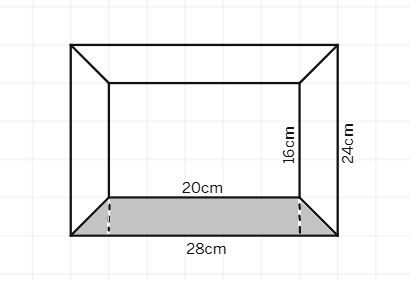
Solution:

Area of the outer rectangle = cm × cm = cm2.

Area of the inner rectangle = cm × cm = cm2.

Area of the shaded part of the frame = Area of outer rectangle - Area of inner rectangle.

Area of the shaded part of the frame = 672 cm2 - 320 cm2.

Area of the shaded part of the frame = cm2.

Therefore, the area of the shaded part of the frame is 352 cm2.

5. Find the area of the field.

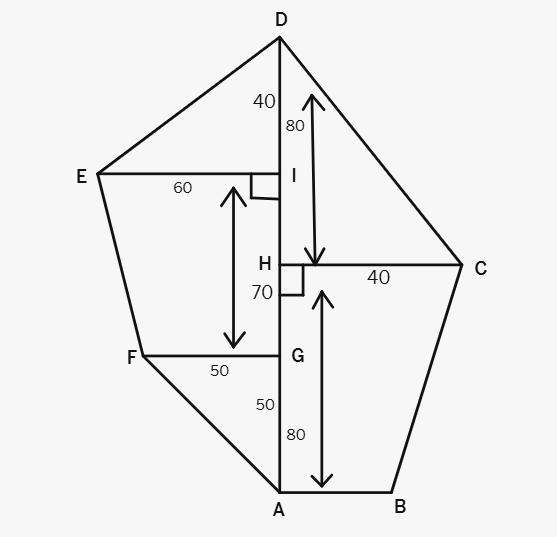
Solution:

Divide the shape into triangles and rectangles.

Triangle ADE: (12) × 60 × 40 = m2.

Triangle ABF: (12) × 50 × 50 = m2.

Rectangle: 40 × 40 = m2.

Triangle BCD: (12) × 40 × 40 = m2.

Triangle EFC: (12) × 20 × 40 = m2. (Assuming 80 - 60 = 20)

Total: 1200 + 1250 + 1600 + 800 + 400 = m2.

6. The ratio of the length of the parallel sides of a trapezium is 5:3 and the distance between them is 16cm. If the area of the trapezium is 960 cm2, find the length of the parallel sides.

Solution:

Let the lengths of the parallel sides be 5x5 and 3x3.

Distance between parallel sides (height) = cm.

Area of trapezium = cm2.

Area of trapezium = (12) × (sum of parallel sides) × height

960 = (12) × ( + ) ×

960 = (12) × (x) × 16

960 = x

x = /64

x =

Length of first parallel side = 5x = 5 × 15 = cm

Length of second parallel side = 3x = 3 × 15 = cm

Therefore, the lengths of the parallel sides are 75 cm and 45 cm.

7. The floor of a building consists of around 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of flooring if each tile costs rupees 20 per m2.

Solution:

Given: Number of tiles =

Diagonal 1 (d1) = cm

Diagonal 2 (d2) = cm

Cost per m2 = Rupees 20

Area of one rhombus tile = (12) × d1 × d2

Area of one rhombus tile = (12) × 45 cm × 30 cm

Area of one rhombus tile = cm2

Total area of 3000 tiles = 3000 × 675 cm2

Total area of 3000 tiles = cm2

Convert cm2 to m2: 1 m2 = 10000 cm2

Total area in m2 = 2025000 cm2 / 10000 cm2/m2

Total area in m2 = m2

Total cost of flooring = Total area in m2 × Cost per m2

Total cost of flooring = 202.5 m2 × Rupees 20m2

Total cost of flooring = Rs.

Therefore, the total cost of flooring is Rs. 4050.

8. There is a pentagonal shaped park as shown in figure. For finding its area Jyothi and Rashida divided it in two different ways. Find the area in both ways and what do you observe?

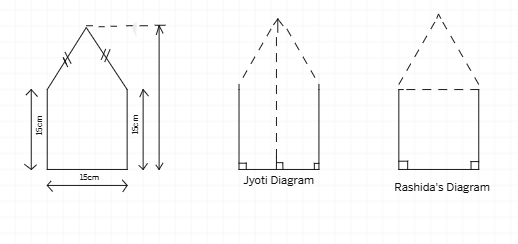
Solution:

Jyothi's Diagram:

Jyothi divides the pentagon into a square and a triangle.

Square Area:

Side = 15 cm

Area = side × side = 15 cm × 15 cm = cm2

Triangle Area:

Base = 15 cm

Height = 15 cm

Area = (12) × base × height = (12) × 15 cm × 15 cm = cm2

Total Area (Jyothi's): 225 cm2+ 112.5 cm2 = cm2

Rashida's Diagram:

Rashida divides the pentagon into two congruent trapezoids.

Trapezoid Area:

Parallel sides: 15 cm and 15 cm

Height = 15 cm2 = cm

Area = (12) × (sum of parallel sides) × height = (12) × (15 cm + 15 cm) × 7.5 cm = cm2

Total Area (Rashida's): 112.5 cm2 × = cm2

There is an error in Rashida's calculation. The total area should be the same in both methods.

Let's correct Rashida's method:

Trapezoid Area:

Parallel sides: 15 cm and 15 cm

Height = 15 cm2 = cm

Area = (12) × (sum of parallel sides) × height = (12) × (15 cm + 15 cm) × 7.5 cm = cm2

Total Area (Rashida's): 112.5 cm2 × 2 = cm2.

The error in Rashida's method was that she only calculated the area of one trapezoid.

Corrected Total Area (Rashida's): 225 cm2 + 112.5 cm2 = cm2

The area of the pentagon is 337.5 cm2 using both methods. The methods are different but the area is the same.