Exercise 7.1

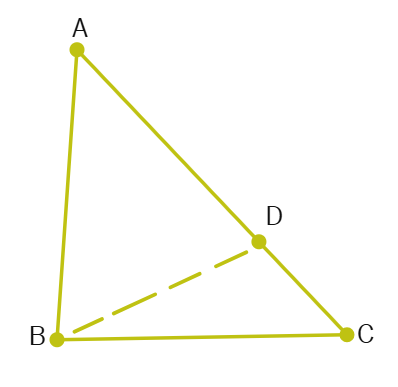
Consider a triangle ABC, where ∠B > ∠C. We need to prove that AC > AB (i.e., the side opposite the larger angle is longer).

On AC, extend the side such that D is a point on BC, and AD = AB.

Now, in ΔABD, we observe that AB = AD (by construction).

Since AD = AB, ΔABD is an triangle, so: ∠ABD = ∠

In a triangle, the side opposite a larger angle is longer, so: > AD

Since AD = AB + and BD = AB, we get: >

Which proves that the side opposite the larger angle is longer.

1. In quadrilateral ACBD, AC = AD and AB bisects ∠A. Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

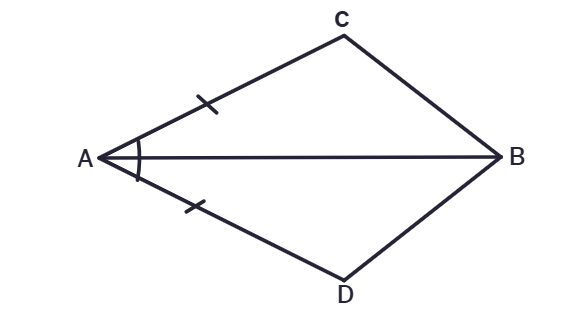
Solution:

Given:

AC = ADAB (Given)

ABAC bisects ∠A (Given)

To Prove:

ΔABC ≅ ΔABD

Proof:

Since AB bisects ∠A, it means that ∠CAB = ∠DAB∠DBA.

Now, consider triangles ΔABC and ΔABD:

AC = (Given)

∠CAB =≠ ∠DAB (AB bisects ∠A)

AB = AB (Common side)

By the Side-Angle-Side (SAS) congruence rule, if two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of another triangle, then the triangles are congruentincongrunet.

Therefore, ΔABC ≅≠ ΔABD (by SASSSS congruence rule).

What can be said about BC and BD?

Since ΔABC ≅ ΔABD, by the Corresponding Parts of Congruent Triangles (CPCT), corresponding sides and angles are equaldifferent.

Therefore, BC = (by CPCT).

In conclusion, ΔABC is congruent to ΔABD, and BC is equal to BD.

2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. Prove that:

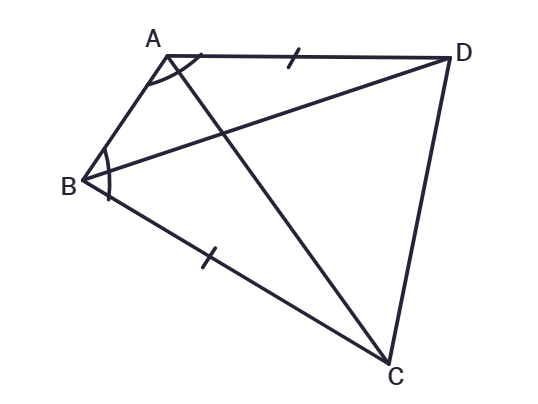
(i) ΔABD ≅ ΔBAC

(ii) BD = AC

(iii) ∠ABD = ∠BAC

Solution:

Given:

AD = BCAB

∠DAB = ∠CBA∠CAB

To Prove:

(i) ΔABD ≅ ΔBAC

In ΔABD and ΔBAC,

= BC (Given)

∠DAB∠DBA = ∠CBA (Given)

AB=ABAD=BC (Common Side)

Therefore, by SASSSSASA congruence rule,

ΔABD ≅ ΔBAC

(ii) BD = AC

Since ΔABD ≅ ΔBAC, by SASCPCT,

BD =

(iii) ∠ABD = ∠BAC

Since ΔABD ≅ ΔBACΔBCD,

∠ABD = ∠BAC∠BCA

3. AD and BC are equal and perpendiculars to a line segment AB. Show that CD bisects AB.

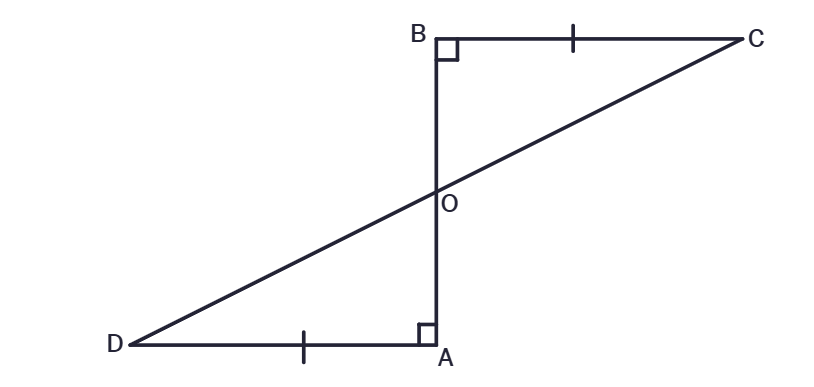
Solution:

Given:

AD = BCAB

AD ⊥ ABCD

BC ⊥ ABCD

To Prove:

CD bisects ABAD

Proof:

In ΔAOD and ΔBOC,

∠DAO = ∠CBO∠BCO (Each 90°)

AD = BCAB (Given)

∠AOD = ∠BOC∠BCO (Vertically opposite angles)

Therefore, by ASASASSSS congruence rule,

ΔAOD ≅ ΔBOCΔABC

Since ΔAOD ≅ ΔBOC, by ASASAS,

AO = BOCO

Therefore, CD bisects .

4. l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that ΔABC ≅ ΔCDA

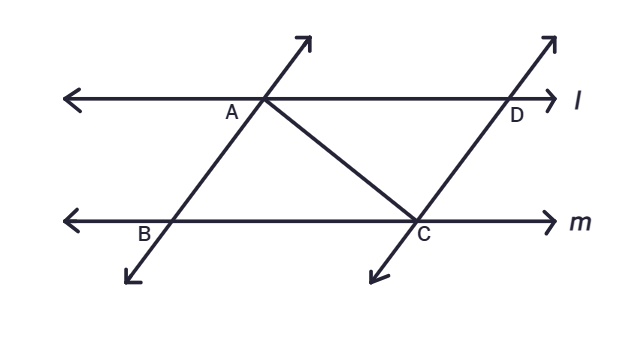
Solution:

Given:

l || mp (l is parallel to m)

p || ql (p is parallel to q)

To Prove:

ΔABC ≅ ΔCDAΔABD

Proof:

In ΔABC and ΔCDA,

∠BAC = ∠DCA∠DAC (Alternate interior angles, l || m)

AC = ACAB (Common side)

∠BCA = ∠DAC∠DCA (Alternate interior angles, p || q)

Therefore, by ASASASSSS congruence rule,

ΔABC ≅ ΔCDA

5. In the adjacent figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

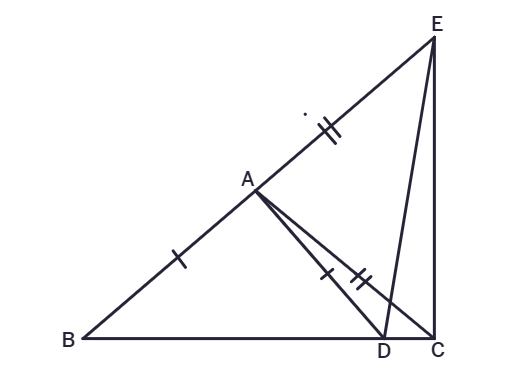
Solution:

Given:

AC = AEAD

AB = ADAE

∠BAD = ∠EAC∠BAC

To Prove:

BC = DECD

Proof:

∠BAD = ∠EAC∠ECA (Given)

Adding ∠DAC to both sides,

∠BAD + ∠DAC∠BAC = ∠EAC + ∠DAC∠DCA

∠BAC = ∠DAE∠EAD

In ΔABC and ΔADE,

AB = ADAE (Given)

AC = AEAD (Given)

∠BAC = ∠DAE∠EAD (Proved above)

{.reveal(when="blank-4")}Therefore, by SASASASSS congruence rule,

ΔABC ≅ ΔADE

Since ΔABC ≅ ΔADE, by SASSSS,

BC = DECD

6. In right triangle ABC, right angle is at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that :

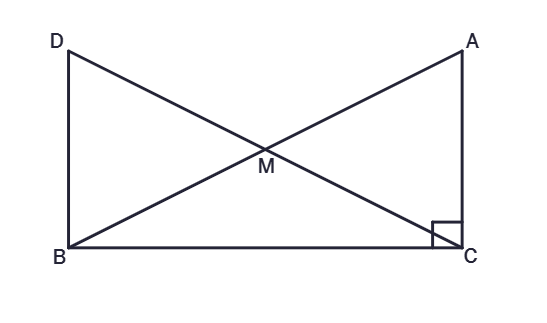
(i) ΔAMC ≅ ΔBMD

(ii) ∠DBC is a right angle

(iii) ΔDBC ≅ ΔACB

(iv) CM = 1/2 AB.

Solution:

Given:

∠ACB = 90°180°

M is the midpoint of ABAC

DM = CMBM

To Prove:

Proof:

(i) ΔAMC ≅ ΔBMD

In ΔAMC and ΔBMD,

AM = BMCM (M is midpoint of AB)

CM = DMAM (Given)

∠AMC = ∠BMD∠CMD (Vertically opposite angles)

Therefore, by SASASASSS congruence rule,

ΔAMC ≅ ΔBMD

(ii) ∠DBC is a right angle

Since ΔAMC ≅ ΔBMD, by SASASA,

∠ACM = ∠BDM∠CDM

AC = BDCD

∠ACB = ∠DBC∠BDC (Alternate interior angles)

Since ∠ACB = 90°, ∠DBC = 90°180°

(iii) ΔDBC ≅ ΔACB

In ΔDBC and ΔACB,

DB = ACBC (Proved above)

BC = BCAC (Common side)

∠DBC = ∠ACB∠ABC (Each 90°)

Therefore, by SASASASSS congruence rule,

ΔDBC ≅ ΔACB

(iv) CM = 1/2 AB

Since ΔDBC ≅ ΔACB, by SASSSS,

DC = ABBC

DM = CM (Given)

DC = + CM = CM + CM =

2CM = ABBC

CM = 1214 AB

7. In the adjacent figure ABCD is a square and ΔAPB is an equilateral triangle. Prove that ΔAPD ≅ ΔBPC.

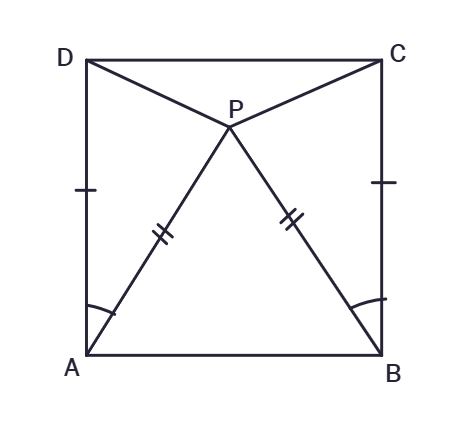
Solution:

Given:

ABCD is a squarerectangle

ΔAPB is an equilateralisosceles triangle

To Prove:

ΔAPD ≅ ΔBPCΔDPC

Proof:

In ΔAPD and ΔBPC,

AD = BCAB (Sides of a square)

AP = BPCP (Sides of an equilateral triangle) {.reveal(when="blank-4")}∠DAB = 90°60° (Angle of a square)

∠PAB = 60°90° (Angle of an equilateral triangle)

∠PAD = ∠DAB - ∠PAB = 90°60° - 60°90° = 30°150°

Similarly, ∠CBA = 90°60° (Angle of a square)

∠PBA = 60°90° (Angle of an equilateral triangle)

∠PBC = ∠CBA - ∠PBA = 90°60° - 60°90° = 30°150°

Therefore, ∠PAD = ∠PBC∠PCB

Thus, by SASASASSS congruence rule,

ΔAPD ≅ ΔBPC

8. In the adjacent figure ΔABC, D is the midpoint of BC. DE ⊥ AB, DF ⊥ AC and DE = DF. Show that ΔBED ≅ ΔCFD.

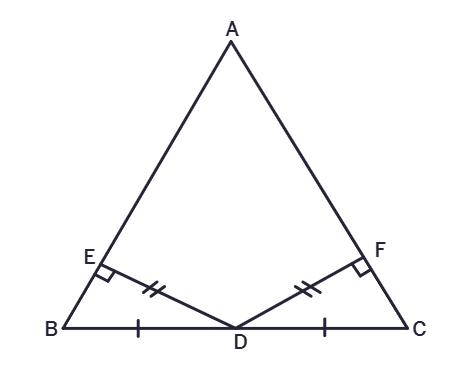
Solution:

Given:

D is the midpoint of BCAB

DE ⊥ ABAC

DF ⊥ ACAB

DE = DFEF

To Prove:

ΔBED ≅ ΔCFDΔDFC

Proof:

In ΔBED and ΔCFD,

∠BED = ∠CFD∠CDF = 90° (Given: DE ⊥ AB and DF ⊥ AC)

BD = CDBC (D is the midpoint of BC)

∠BDE = ∠CDF∠DCF (Since DE ⊥ AB and DF ⊥ AC, ∠BDE and ∠CDF are either alternate interior angles or corresponding angles depending on whether AB || AC. If AB || AC, they are alternate interior angles. If not, they are corresponding angles.)

Therefore, by AASASASAS congruence rule (Angle-Angle-Side),

ΔBED ≅ ΔCFD

9. If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.

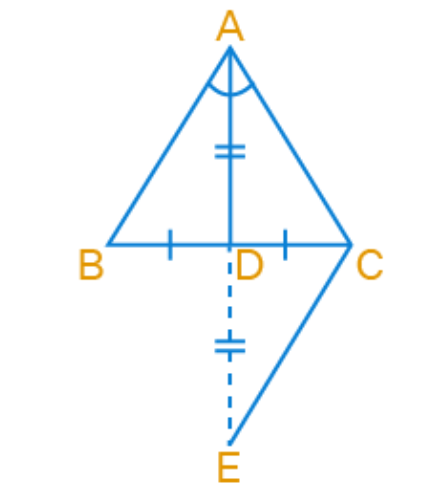
Solution:

Given:

Triangle ABC.

AD is the angle bisector of ∠BAC.

AD bisects , meaning BD = .

To Prove:

Triangle ABC is isosceles (AB = AC).

Construction:

Extend AD to point E such that AD = .

Join CE.

Proof:

In ΔADB and ΔEDC:

BD = (Given)

∠ADB = ∠EDC∠ECD (Vertically opposite angles)

AD = (By construction)

By SASSSSASA congruence rule, ΔADB ≅ ΔEDC.

Therefore, AB = CECD (CPCTC).

Also, ∠BAD = ∠CED∠CDE (CPCTC).

Given that AD is the bisector of ∠BAC, ∠BAD = ∠CAD∠CDA.

From above, ∠CAD = ∠CED∠CDE.

In ΔAEC, ∠CAD = ∠CED, so AC = (Sides opposite to equal angles are equal).

From above, AB = CE and AC = CE. Therefore, AB = .

Hence, triangle ABC is isosceles.

10. In the given figure ABC is a right triangle and right angled at B such that ∠BCA = 2∠BAC. Show that hypotenuse AC = 2BC. (Hint : Produce CB to a point D that BC = BD)

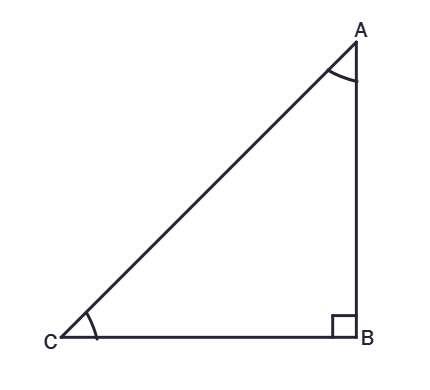
Solution:

Given:

ΔABC is a right triangle, ∠ABC = 90°180°

∠BCA = 2∠BACABC

BC = BDAD (By construction)

To Prove:

AC = 2BCAB

Proof:

In ΔABC and ΔABD,

BC = BDAD (By construction)

∠ABC = ∠ABD∠ADB = 90°

AB = ABAC (Common side)

Therefore, by SASASASSS congruence rule,

ΔABC ≅ ΔABD

Since ΔABC ≅ ΔABD, by CPCTSAS,

AC = ADCD

∠BAC = ∠BAD∠BDA

∠CAD = ∠BAC + ∠BAD = 2∠BACABC

∠BCA = 2∠BAC (Given)

∠CAD = ∠BCA∠ABC

In ΔACD,

∠CAD = ∠ACD

AD = CDAC (Sides opposite to equal angles are equal)

AC = AD (Proved above)

AC = CD

CD = CB + BDAD

CD = BC + BC = 2BCAB

AC = 2BC