Exercise 7.3

1. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:

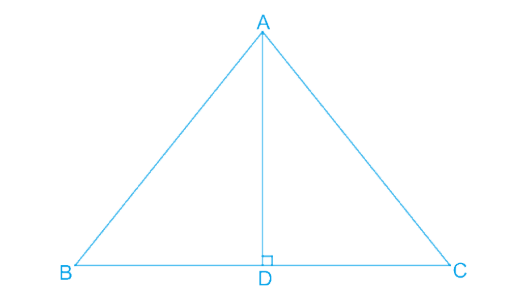
(i) AD bisects BC

(ii) AD bisects ∠A.

Solution:

Given:

ABC is an isosceles triangle with AB = .

AD is the altitude from A to .

Proof:

AD bisects

In ΔADB and ΔADC:

∠ADB = ∠ADC = 90°180° (AD is the altitude)

AB = ] (Given)

AD = (Common side)

By RHS congruence rule, ΔADB ≅ ΔADC.

Therefore, BD = (CPCTC). Hence, AD bisects .

AD bisects

Since ΔADB ≅ ΔADC (Proved above), ∠BAD = ∠CAD∠CDA (CPCTC).

Therefore, AD bisects ∠A.

2. Two sides AB, BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR. Show that:

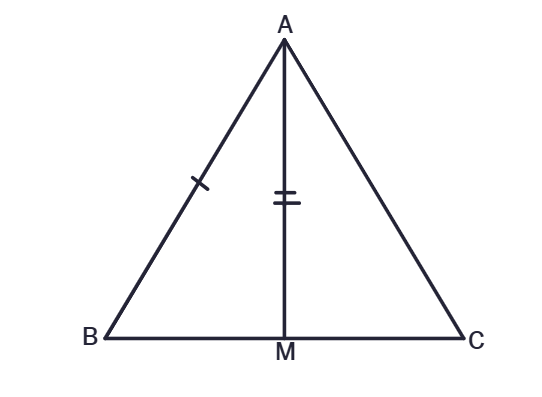
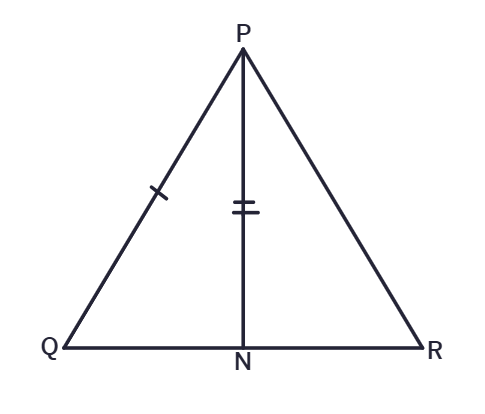
(i) ΔABM ≅ ΔPQN (ii) ΔABC ≅ ΔPQR

Solution:

AB =

BC =

AM = (where AM and PN are medians)

(i) ΔABM ≅ ΔPQN

BM = 12BCBC (AM is a median)

QN = 12QRQR (PN is a median)

BC = (Given)

Therefore, BM =

AB = (Given)

AM = (Given)

By SSSSASAAS congruence rule, ΔABM ≅ ΔPQNΔPQR.

(ii) ΔABC ≅ ΔPQR

ΔABM ≅ ΔPQN (Proved above)

∠ABM = ∠PQN∠PNQ (CPCTC)

∠ABC = ∠PQR∠PRQ (∠ABM and ∠PQN are the same angles as ∠ABC and ∠PQR respectively)

AB = (Given)

BC = (Given)

By SAS congruence rule, ΔABC ≅ ΔPQRΔPQN.

3. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

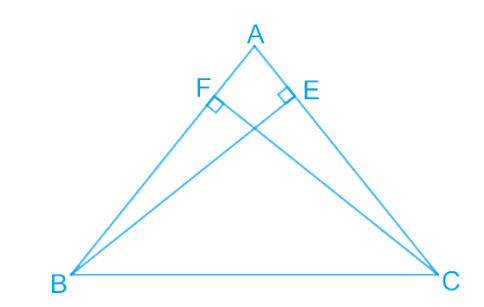
Solution:

Given:

BE and CF are altitudes of ΔABC.

BE = .

To Prove:

ΔABC is isosceles (i.e., AB = AC).

Proof:

In ΔBCE and ΔCBF:

∠BEC = ∠CFB = 90°180° (Given, BE and CF are altitudes)

BC = BC (Common side)

BE = CFCE (Given)

By RHSSASSSS congruence rule, ΔBCE ≅ ΔCBF.

Therefore, ∠BCE = ∠CBF∠CFB (CPCTC).

∠BCE is the same as ∠ACB, and ∠CBF is the same as ∠ABC.

So, ∠ACB = ∠ABC∠ACE.

In ΔABC, ∠ACB = ∠ABC. Therefore, AB = (Sides opposite to equal angles are equal).

Therefore, ΔABC is isosceles.

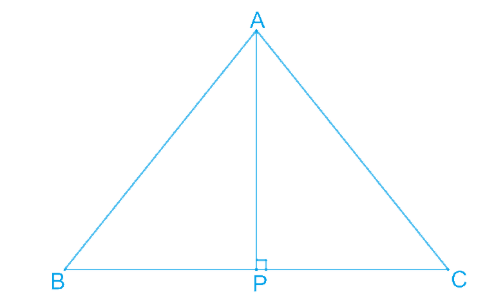
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.

Solution:

Given:

ABC is an isosceles triangle with AB = .

AP ⊥

To Prove:

∠B = ∠C

Proof:

In ΔABP and ΔACP:

∠APB = ∠APC = 90°180° (AP is the altitude)

AB = (Given)

AP = AP (Common side)

By RHSSASSSS congruence rule, ΔABP ≅ ΔACP.

Therefore, ∠B = ∠C∠D (CPCTC).

∠B = ∠C in the isosceles triangle ABC.

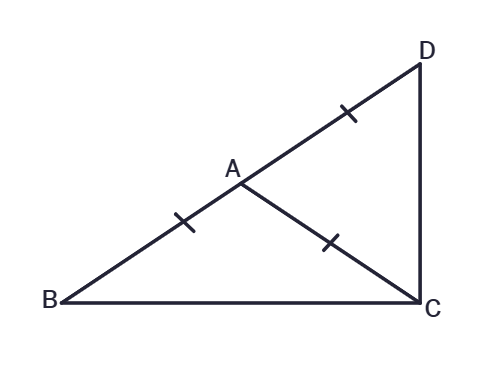
5. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB. Show that ∠BCD is a right angle.

Solution:

Given:

ΔABC is isosceles with AB = .

BA is produced to D such that AD = .

To Prove:

∠BCD = 90°

Proof:

Given AB = AC, in ΔABC:

∠ABC = ∠ACB∠ABC (Angles opposite to equal sides are equal)

Given AD = , in ΔADC:

∠ACD = ∠ADC∠ACD (Angles opposite to equal sides are equal)

In ΔBCD, the sum of all angles is 180°360°:

∠BCD + ∠CDB + ∠DBC∠BAC = 180°90°

∠DBC = ∠ABC∠ACD and ∠CDB = ∠ADC∠ACB:

∠BCD + ∠ADC + ∠ABC = 180°

Substitute ∠ACB for ∠ABC and ∠ACD for ∠ADC:

∠BCD + ∠ACD∠ADC + = 180°

Where ∠BCD = ∠ACB∠ABC + ∠ACD:

∠BCD + ∠BCD∠BDC = 180°

∠BCD = 180°

∠BCD = 180°/2180°

∠BCD = 90°80°

Therefore, ∠BCD is a right angle.

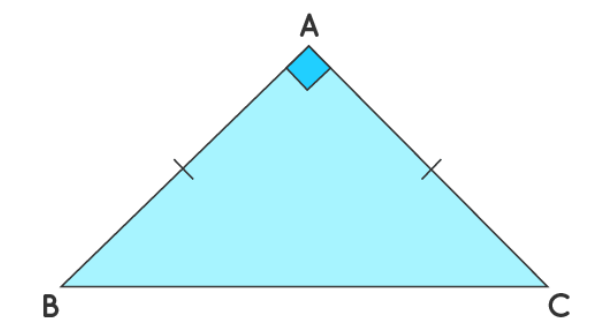
6. ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Show that ∠B = ∠C.

Solution:

Given:

ABC is a right-angled triangle.

∠A = 90°180°

AB =

To Prove:

∠B = ∠C

Proof:

Since AB = AC, triangle ABC is an isoscelesequilateral right-angled triangle.

In an isosceles triangle, the angles opposite to the equal sides are equalnot equal.

∠B = .

Therefore, in the right-angled triangle ABC, where AB = AC, it is shown that ∠B = ∠C.

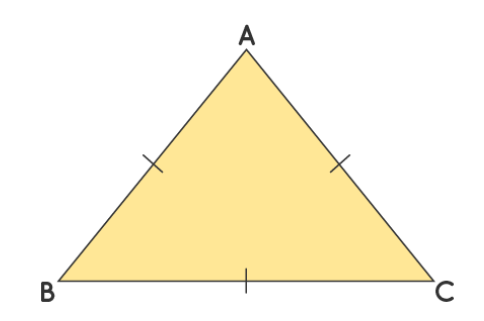
Show that the angles of an equilateral triangle are 60° each.

Solution:

Given:

Triangle ABC is an equilateral triangle. This means AB = BC = .

To Prove:

∠A = ∠B = ∠C = 60°

Proof:

Since AB = BC, ∠C = ∠A∠B (Angles opposite to equal sides are equal).

Since BC = CA, ∠A = ∠B∠A (Angles opposite to equal sides are equal).

Therefore, ∠A = ∠B = ∠C.

Now, in ΔABC,

∠A + ∠B + ∠C = 180°360° (Angle sum property of a triangle)

Since ∠A = ∠B = ∠C, we can write:

∠A + ∠A + ∠A = 180°

∠A = 180°

∠A = 60°50°

So, ∠A = ∠B = ∠C = 60°.

Therefore, the angles of an equilateral triangle are 60° each.

8. In the adjacent figure ΔABC is isosceles as AB=AC, BA and CA are produced to Q and P such that AQ=AP. Show that PB=QC.

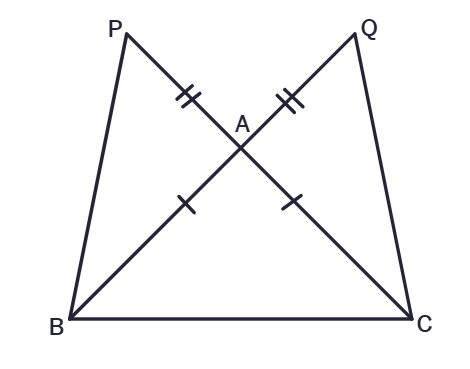
(Hint : Compare ΔAPB and ΔAQC)

Solution:

Given:

ΔABC is isosceles with AB = .

BA is produced to and is produced to P.

AQ = .

To Prove:

PB = QC

Proof:

Consider ΔAPB and ΔAQC:

AP = (Given)

AB = AC (Given)

∠PAB = ∠QAC∠QCA (Vertically opposite angles)

Therefore, by SASSSSAAS congruence rule, ΔAPB ≅ ΔAQC.

Hence, PB = (Corresponding parts of congruent triangles are equal - CPCTC).**

Conclusion:

We have shown that PB = QC.