Inequalities in a Triangle
Activity One:
Consider the triangle above. Move the vertices around to get different triangle. Create three different triangles like that and fill up the values for one triangle below.
Check for different triangles.
| Side1 | Side2 | Side3 | Side1+Side2 | Side1-Side2 |
|---|---|---|---|---|
| AB = | BC = | CA = | AB+BC = | AB-BC= |
| BC = | CA= | AB= | BC+CA= | BC-CA= |
| CA= | AB= | BC= | CA+AB= | CA-AB= |
For different values of the 3 sides, what do you observe ? The sum of two sides is more than the third side.
Also, the difference of two sides is
Therefore, we conclude that:
Triangle Inequality Theorem:
This theorem states that in any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
Mathematically, for a triangle with sides a, b and c, this means:
a + b > c and b + c > a and c + a > b
This principle is crucial for the existence of a triangle. If this condition is not met, a triangle cannot be formed.
We also find that:
Side Length Difference:
The difference between the lengths of any two sides of a triangle must be less than the length of the third side. This can be seen as a corollary to the Triangle Inequality Theorem.
Mathematically, it is represented as:
∣a−b∣ < c
∣b−c∣ < a
∣c−a∣ < b
This condition ensures that the two shorter sides are sufficiently long to meet and form a triangle with the third side.
Theorem: If two sides of a triangle are unequal, the angle opposite to the longer side is larger.
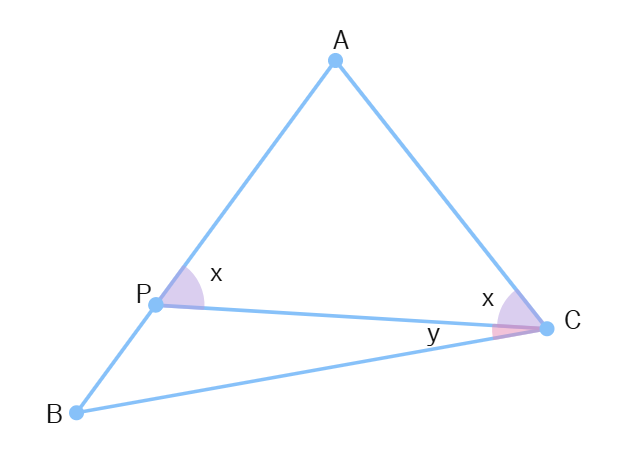
Let us assume a triangle ABC such that the sides are as AB > AC.
By theorem, we need to prove that angle C > angle B.
Now, take a point P on line AB such that AP = AC. Join the two points C and P to set CP. Let us assume angle APC is x° and angle BCP is y°.
We know that AP =
Mathematically, we write these steps as follows:
∠ACP = ∠
∠ACP =
On line AB, we can say that it is a straight line which is equal to
∠ACP + ∠CPB = 180°
By substituting the value of angle APC, we get the equation as: x + ∠CPB = 180°
By subtracting x on both the sides of the equation, we get it as: ∠CPB = 180° -
We know the theorem that sum of all the angles in a triangle is
∠BCP + ∠CPB + ∠CBP = 180°
By applying this to the triangle CPB, we get it as,
∠BCP +
∠CBP =
From the diagram, we can say that,
∠CBP = ∠
∠CBA = x - y
From the diagram, we can say that,
∠BCA = ∠BCP + ∠PCA
By substituting the values, we get it in the form of
∠BCA =
From (i) and (ii), we can say the inequality in the form of:
∠BCA > ∠CBA
∠C > ∠B
Hence, we have proved that the angle opposite to the greater side is larger.
