Exercise 7.2
1. In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at O. Join A to O. Show that :
(i) OB = OC
(ii) AO bisects ∠A
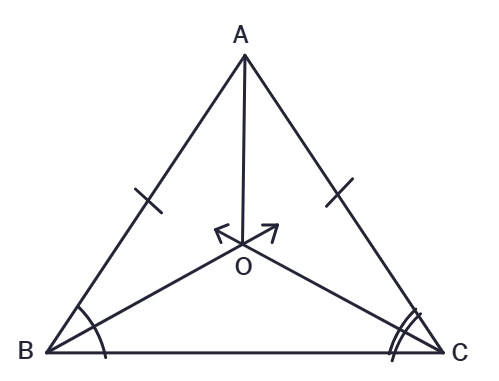
Solution:
Given:
ΔABC is
OB is the bisector of
OC is the bisector of
To Prove:
(i) OB =
(ii) AO bisects
Proof:
{.reveal(when="blank-3")}(i) OB = OC
In ΔABC,
AB = AC (Given)
∠ABC =
1/2 ∠ABC = 1/2
∠OBC =
OB =
(ii) AO bisects ∠A
In ΔAOB and ΔAOC,
AB =
OB =
AO =
Therefore, by
ΔAOB ≅ ΔAOC
Since ΔAOB ≅ ΔAOC, by
∠BAO =
Therefore, AO bisects
2. In ΔABC, AD is the perpendicular bisector of BC (See adjacent figure). Show that ΔABC is an isosceles triangle in which AB = AC.
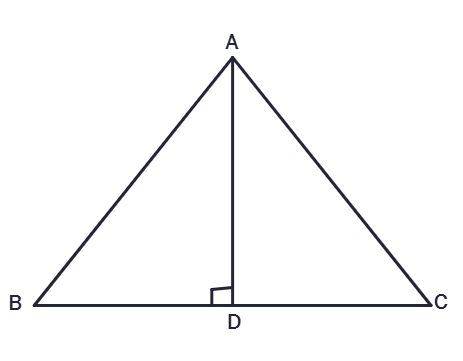
Solution:
Given:
AD is the perpendicular bisector of
To Prove:
ΔABC is
Proof:
In ΔADB and ΔADC,
BD =
∠ADB =
AD =
Therefore, by
ΔADB ≅ ΔADC
Since ΔADB ≅ ΔADC, by
AB =
Therefore, ΔABC is
3. ABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
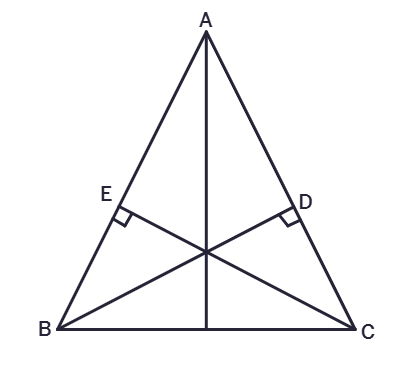
Solution:
Given:
ΔABC is
BD ⊥
CE ⊥
To Prove:
BD =
Proof:
In ΔBEC and ΔCDB,
∠BEC = ∠CDB =
BC =
∠EBC =
Therefore, by
ΔBEC ≅ ΔCDB
Since ΔBEC ≅ ΔCDB, by
BD =
4. ABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that:

(i) ΔABD ≅ ΔACE
(ii) AB = AC i.e., ABC is an isosceles triangle.
Solution:
Given:
BD ⊥
CE ⊥
BD =
To Prove:
(i) ΔABD ≅ ΔACE
In ΔABD and ΔACE,
∠ADB =
BD =
∠BAD =
Therefore, by
ΔABD ≅ ΔACE
(ii) AB = AC
Since ΔABD ≅ ΔACE, by
AB =
__Therefore, ΔABC is
5. ΔABC and ΔDBC are two isosceles triangles on the same base BC (see figure). Show that ∠ABD = ∠ACD.
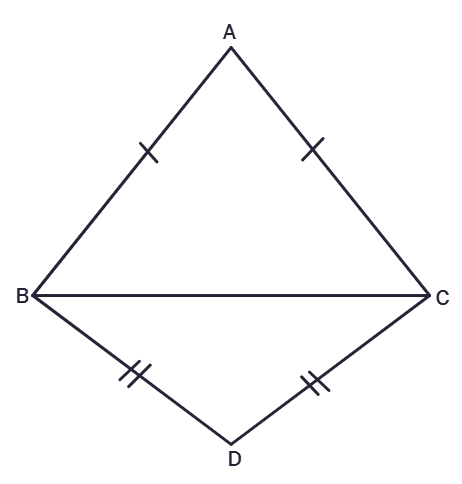
Solution:
Given:
ΔABC is
ΔDBC is
To Prove:
∠ABD =
Proof:
In ΔABD and ΔACD,
AB =
BD =
AD =
Therefore, by
ΔABD ≅ ΔACD
Since ΔABD ≅ ΔACD, by
∠ABD =
