Exercise 7.4

Show that in a right-angled triangle, the hypotenuse is the longest side.

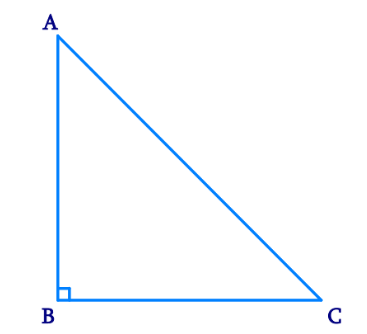
Solution:

Given:

A right-angled triangle ABC, where ∠B =

To Prove:

AC (the hypotenuse) is the longest side.

Proof:

In ΔABC,

∠A + ∠B + ∠C = 180°90° (Angle sum property of a triangle)

∠A + 90°180° + ∠C = 180°

∠A + ∠C = 90°180°

This shows that ∠A and ∠C are both acuteobtuse angles (less than 90°).

Since ∠B = 90° and ∠A and ∠C are acute angles, ∠B is the largestsmallest angle in ΔABC.

We know that in any triangle, the side opposite to the largest angle is the longestshortest side.

Therefore, AC (the side opposite to ∠B) is the longest side in ΔABC.

In a right-angled triangle, the hypotenuseadjacent is the longest side.

2. In adjacent figure, sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

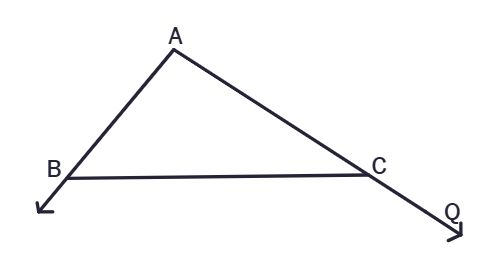
Solution:

Given:

∠PBC <

Sides AB and AC are extended to P and Q.

To Prove:

AC >

Proof:

∠ABC + ∠PBC = (Linear Pair)

∠ACB + ∠QCB = (Linear Pair)

Given ∠PBC < ∠QCB

Therefore, ∠ABC >

AC > (Side opposite to larger angle is longer)

3. In adjacent figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

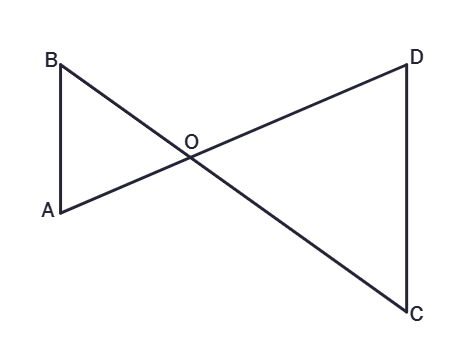
Solution:

Given:

∠B <

∠C <

To Prove:

AD <

Proof:

In ΔAOD, ∠B < ∠A

Therefore, AO < (Side opposite to smaller angle is smaller)

In ΔBOC, ∠C < ∠D

Therefore, BO < (Side opposite to smaller angle is smaller)

AO + DO <

AD <

4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD. Show that ∠A > ∠C and ∠B > ∠D.

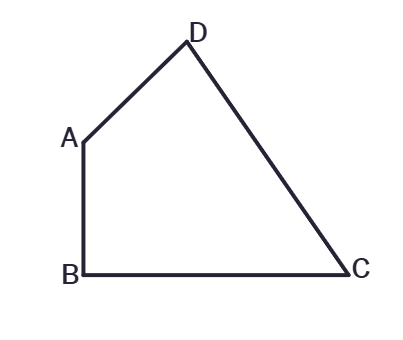
Solution:

Given:

AB is the side.

CD is the side.

To Prove:

∠A >

∠B >

Proof:

Join AC.

In ΔABC, AB <

∠ACB > (Angle opposite to longer side is larger) -- (1)

In ΔADC, AD <

∠CAD > (Angle opposite to longer side is larger) -- (2)

Adding (1) and (2), ∠ACB + ∠CAD >

∠A >

Similarly, by joining BD, we can prove ∠B >

5. In adjacent figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

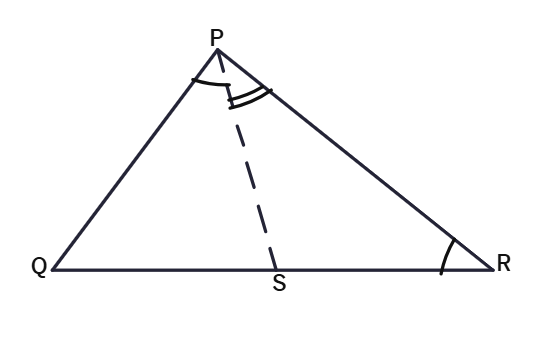
Solution:

Given:

PR >

PS bisects ∠QPR.

To Prove:

∠PSR >

Proof:

PR > PQ (Given)

∠PQS > (Angle opposite to longer side is larger) -- (1)

PS bisects ∠QPR

∠QPS = -- (2)

In ΔPQS, ∠PSQ = 180° - (∠PQS + ) -- (3)

In ΔPRS, ∠PSR = 180° - (∠PRS + ) -- (4)

From (1) and (2), ∠PQS > ∠PRS and ∠QPS = ∠RPS

Therefore, ∠PSQ < (From (3) and (4))

∠PSR >

6. If two sides of a triangle measure 4cm and 6cm find all possible measurements (positive integers) of the third side. How many distinct triangles can be obtained?

Solution:

Understanding the Triangle Inequality:

In any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.

Applying the Triangle Inequality:

Let the third side of the triangle be represented by 'x'. We need to find the possible values of 'x' that satisfy the triangle inequality.

Case 1: 4 + 6 > x => 10 > x

Case 2: 4 + x > 6 => x > 2

Case 3: 6 + x > 4 => x > -2 (This condition is always true for positive values of x)

Combining the relevant conditions, we get:

2 < x < 10

Possible Integer Values for the Third Side:

The possible integer values for 'x' that satisfy the above inequality are:

3, 4, 5, 6, 7, 8, and 9.

Distinct Triangles:

Since the order of the sides does not matter in forming a triangle (i.e., 4, 6, and 7 form the same triangle as 6, 7, and 4), we have 7 distinct triangles possible.

Conclusion:

The possible measurements (positive integers) for the third side are 3, 4, 5, 6, 7, 8, and 9. Seven distinct triangles can be obtained.

7. Try to construct a triangle with 5cm, 8cm and 1cm. Is it possible or not? Why? Give your justification?

Solution:

Triangle Inequality Theorem:

The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greaterlower than the length of the third side.

Checking the Given Sides:

Let's check if the given sides (5cm, 8cm, and 1cm) satisfy the Triangle Inequality Theorem:

5cm + 8cm > 1cm (TrueFalse)

5cm + 1cm > 8cm (FalseTrue)

8cm + 1cm > 5cm (TrueFalse)

Since one of the conditions (5cm + 1cm > 8cm) is false, the given sides satisfynot satisfy the Triangle Inequality Theorem.

Therefore, it is not possible to construct a triangle with sides of 5cm, 8cm, and 1cm. This is because the sum of the lengths of the two shorter sides (5cm and 1cm) is not greater than the length of the longest side (8cm), violating the Triangle Inequality Theorem.