Enhanced Curriculum Support
This is a comprehensive educational resource designed to provide students with the tools and guidance necessary to excel. This support system is structured to cater to various aspects of learning, ensuring that students are well-prepared for academic challenges and practical applications of mathematical concepts. Some are the key benefits are mentioned below:
Comprehensive Learning: This holistic approach helps students gain a thorough understanding of the subject. Practical Application: The resources encourage students to apply mathematical concepts to real-life scenarios, enhancing their practical understanding and problem-solving skills.
Critical Thinking and Reasoning: Value-Based and HOTS questions promote critical thinking and reasoning abilities. These skills are crucial for students to tackle complex problems and make informed decisions.
Exam Preparedness: Sample Question Papers and Practice Questions provide ample practice for exams. They help students familiarize themselves with the exam format and types of questions, reducing exam anxiety.
Ethical and Moral Development: Value-Based Questions integrate ethical and moral lessons into the learning process, helping in the overall development of students' character and social responsibility. By incorporating these diverse elements, Enhanced Curriculum Support aims to provide a robust and well-rounded knowledge, preparing students for both academic success and real-world challenges.
Sample Questions
Sec A
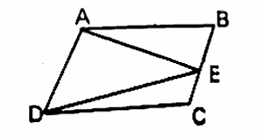
(1) In the given figure, area of △MDE is 24 sq.cm, then the area of △ABCD:
(A) 24 sq.cm (B) 48 sq.cm (C) 12 sq.cm (D) 36 sq.cm
(2) Find the area of a parallelogram whose base is 12 cm and height is 8 cm.
(3) A triangle has an area of 24
(4) State whether the following statement is true or false. Justify your answer: “If two parallelograms lie on the same base and have equal areas, they lie between the same parallels.”
(5) Triangle ABC and triangle ABD are on the same base AB. CD is bisected by AB at point O. Show that area(△ABC) = area(△ABD).
Sec B
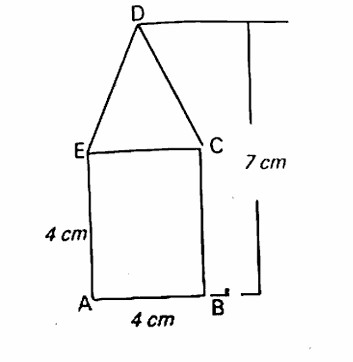
(1) Find the area of pentagon ABCDE from the figure.
(2) ABCD is a parallelogram, and triangle DEF is drawn such that both lie on the same base and between the same parallels. Prove that area(△DEF) =
(3) A triangle and a parallelogram are drawn on the same base of 10 cm and between the same parallels. If the height of the parallelogram is 6 cm, find the area of both figures.
(4) A pentagon is divided into two triangles and a parallelogram. If the areas of the triangles are 18
(5) Two parallelograms have the same area of 72
(6) Show that the area of triangle is invariant even if it is tilted, provided it lies between the same base and same parallels. Draw suitable diagrams to explain your answer.
Sec C
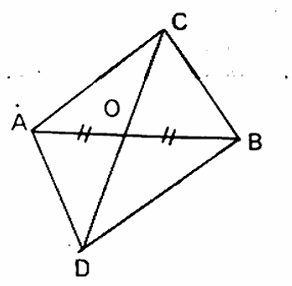
(1) In the following figure, △ABC and △ABD are two triangles on the same base AB. If the line segment CD is bisected by AB at 'O'. Show that area (△ABC) = area (△ABD).
Value Based Questions
Problem 1
A group of students is planting saplings in triangular plots of land. They ensure all triangles are on the same base and between the same parallels, even though the shape and orientation look different. How is this linked to the value of equality and unbiased distribution of resources?
Problem 2
A team decorating a stage uses different shapes but equal area for each decoration to maintain balance. Why is it important in design and planning to understand that congruent shapes are equal in area, but equal areas do not imply congruence? How does this reflect the value of thoughtful planning?
Problem 3
In a geometry art competition, students must use paper cut-outs of triangles and parallelograms of equal area. One student uses rectangles instead and wins. The others protest. What lesson can be learned about defining fairness and following rules based on geometry?
HOTS
Q1
A triangle and a parallelogram are on the same base and between the same parallels. Without knowing the actual dimensions, can you find a relationship between their areas? Justify geometrically.
Q2
You are given three triangles on the same base but only two lie between the same parallels. Can all three have equal areas? Explain with a figure and reasoning.
Q3
A quadrilateral is split into two triangles by one of its diagonals. If the two triangles lie between the same parallels and on equal bases, what can you say about the original quadrilateral? Support your answer with an area argument.
Q4
If two parallelograms lie on the same base and have equal areas but do not lie between the same parallels, what does that tell us? Explain why the converse of “same base and same parallels ⇒ equal area” does not hold.
Q5
A triangle is divided into two smaller triangles by joining a point on one side to the opposite vertex. If the point is the midpoint, can you say the two triangles are equal in area? Why or why not? Use reasoning based on congruence and area formula.
Practice Questions
Choose the correct option.
Questions
(1) Two figures are said to be on the same base and between the same parallels if:
(A) They have same number of sides (B) They are congruent (C) They have a common base and their opposite vertices lie on a line parallel to the base (D) They have equal areas
(2) Area of a parallelogram =
(A)
(3) If a triangle and a parallelogram are on the same base and between the same parallels, then:
(A) The triangle has double the area of the parallelogram (B) The triangle has half the area of the parallelogram (C) Both have equal areas (D) Area of triangle is three times the area of parallelogram
(4) If two parallelograms lie between the same parallels and on the same base, then:
(A) One has larger area (B) They are congruent (C) They are equal in area (D) Nothing can be said
(5) If the area of a parallelogram is 48 cm² and its base is 8 cm, then its height is:
(A) 6 cm (B) 8 cm (C) 12 cm (D) 4 cm
Fill in the blanks.
Questions
(1) Area of triangle = ? × base × height
(2) Two congruent figures have ? areas.
(3) The area of a triangle on the same base and between the same parallels as a parallelogram is ? the area of the parallelogram.
(4) The unit of area is always in ? units.
(5) If two parallelograms are on the same base and have equal areas, they lie between the ? parallels.
State True or False.
Questions
All figures that have equal area are also congruent.
Parallelograms with the same base and lying between the same parallels are equal in area.
The area of a figure refers to the length of its boundary.
A triangle lying on the same base and between the same parallels as a parallelogram has equal area.
Area of parallelogram = base × height.
Answer the following questions.
Questions
(1) Find the area of a triangle with base 10 cm and height 6 cm.
(2) The area of a parallelogram is 60 cm² and its height is 5 cm. Find the length of its base.
(3) Two parallelograms have equal areas of 80 cm². If one has a base of 10 cm, and the other has a base of 8 cm, find the height of each.
(4) A triangle and a parallelogram lie on the same base of 12 cm and between the same parallels. If the height of the parallelogram is 5 cm, find the area of the triangle.
(5) A figure is made by joining a parallelogram and a triangle. If the parallelogram has an area of 36 cm² and the triangle has an area of 18 cm², what is the total area of the figure?
Case Based Questions
Q1
A designer is laying tiles in a hall using triangular and parallelogram-shaped tiles. Both shapes are of the same base and placed between the same boundaries.
Triangle tile base = 12 cm
Parallelogram tile base = 12 cm
Height for both = 6 cm
(a) Find the area of each tile.
(b) How many triangle tiles will be needed to cover the same area as 10 parallelogram tiles?
(c) If a triangle tile costs ₹3 and a parallelogram tile costs ₹5, which option is more cost-efficient per unit area?
Q2
A student cuts a large triangle into two smaller figures: a triangle and a parallelogram. All pieces lie between the same parallels and share common bases.
(a) If the area of the large triangle is 60 sq.cm and the triangle piece is 20 sq.cm, find the area of the parallelogram.
(b) Can the triangle and parallelogram be congruent in this setup? Why or why not?
(c) Which property of area is used to solve this problem?
Q3
A farmer divides a quadrilateral-shaped field into two triangles by drawing a diagonal. He finds the base and height of both triangles to be the same.
(a) Will the two triangles have equal areas?
(b) If one triangle is fenced and the other isn’t, how much fencing material is needed for the fenced part if each side is 30 m?
(c) If the farmer wants to equally distribute seeds in both parts, is it mathematically fair?
