Exercise 11.1

1. In ΔABC, ∠ABC = 90°, AD = DC, AB = 12cm and BC = 6.5 cm. Find the area of ΔADB.

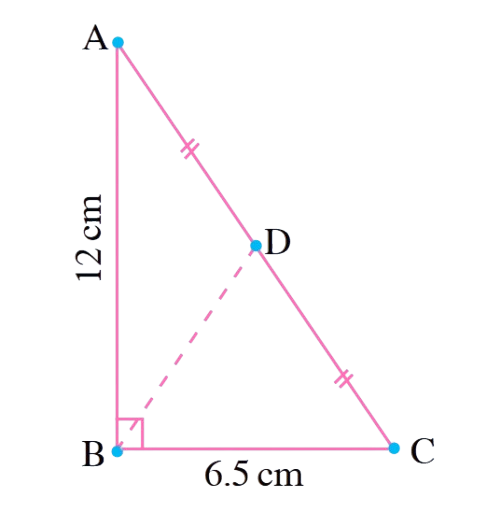
Solution:

First, let's find AC using the Pythagorean theorem in right triangle ABC.

AC² = AB² + BC² = +

AC² = + =

AC = cm (approximately)

Since AD = DC, D is the of AC.

So AD = AC/2 = cm

To find the area of ΔADB, we need the height from D to AB.

Since D is the midpoint of AC, the height from D to AB is half the height from C to AB.

Height from C to AB = cm (which is BC)

Height from D to AB = cm

Area of ΔADB = (1/2) × base × height = (1/2) × ×

Area of ΔADB = cm²

2. Find the area of a quadrilateral PQRS in which ∠QPS = ∠SQR = 90°, PQ = 12 cm, PS = 9 cm, QR = 8 cm and SR = 17 cm (Hint: PQRS has two parts).

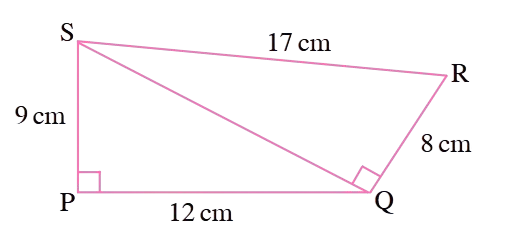
Solution:

The quadrilateral can be divided into two right triangles: ΔPQS and ΔQRS.

For right triangle PQS:

• PQ = cm

• PS = cm

• ∠QPS = °

Area of ΔPQS = (1/2) × PQ × PS = (1/2) × × = cm²

For right triangle QRS:

• QR = cm

• SR = cm

• ∠SQR = °

We need to find QS using Pythagorean theorem in ΔPQS:

QS² = PQ² + PS² = + = + =

QS = cm

Now in right triangle QRS:

Area of ΔQRS = (1/2) × QR × QS = (1/2) × × = cm²

Total area of quadrilateral PQRS = Area of ΔPQS + Area of ΔQRS

= + = cm²

3. Find the area of trapezium ABCD as given in the figure in which ADCE is a rectangle. (Hint: ABCD has two parts).

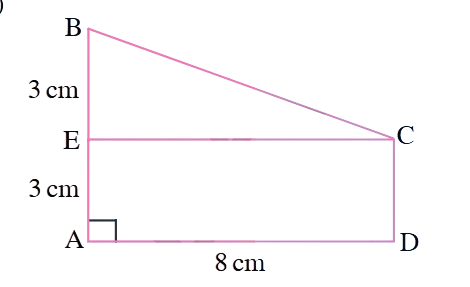
Solution:

The trapezium ABCD can be divided into:

1. Rectangle ADCE

2. Triangle BCE

From the figure:

• AD = EC = cm (opposite sides of rectangle)

• AE = DC = cm (opposite sides of rectangle)

• BE = cm

Area of rectangle ADCE = length × width = × = cm²

For triangle BCE:

- Base EC = cm

- Height BE = cm

Area of triangle BCE = (1/2) × base × height = (1/2) × × = cm²

Total area of trapezium ABCD = Area of rectangle ADCE + Area of triangle BCE

= + = cm²

4. ABCD is a parallelogram. The diagonals AC and BD intersect each other at 'O'. Prove that ar(ΔAOD) = ar(ΔBOC). (Hint: Congruent figures have equal area).

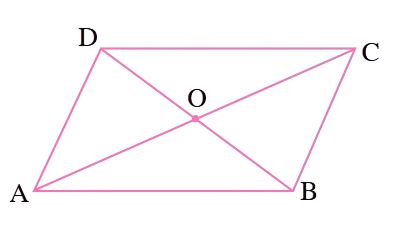
Solution:

To prove: ar(ΔAOD) = ar(ΔBOC)

In parallelogram ABCD, we know that:

• Opposite sides are and

• Diagonals each other

Since diagonals bisect each other at O:

- AO =

- BO =

In triangles ΔAOD and ΔBOC:

- AO = (diagonals bisect each other)

- BO = (diagonals bisect each other)

- ∠AOD = (vertically opposite angles)

By congruence criterion:

ΔAOD ≅ Δ

Since congruent figures have areas:

ar(ΔAOD) = ar(ΔBOC)

Hence proved.