Exercise 11.3

1. In a triangle ABC (see figure), E is the midpoint of median AD, show that

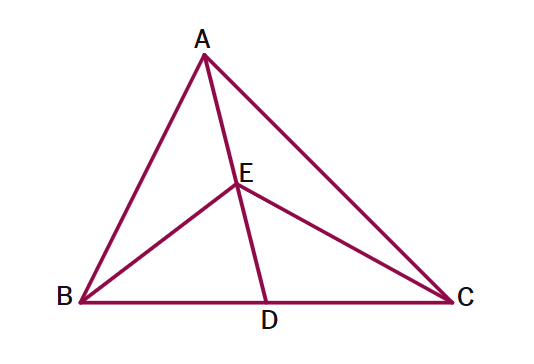
(i) ar(ΔABE) = ar(ΔACE)

(ii) ar(ΔABE) = (1/4)ar(ΔABC)

Solution:

(i) To prove: ar(ΔABE) = ar(ΔACE)

Since AD is a median of triangle ABC, D is the of BC.

Therefore: ar(ΔABD) = ar(ΔACD) = ar(ΔABC)

Since E is the midpoint of AD:

- AE =

- Triangles ABE and ACE have equal heights from B and C to line

In triangle ABD: Since E is midpoint of AD, ar(ΔABE) = ar(ΔABD)

In triangle ACD: Since E is midpoint of AD, ar(ΔACE) = ar(ΔACD)

Since ar(ΔABD) = ar(ΔACD), we get: ar(ΔABE) = ar(ΔACE)

(ii) To prove: ar(ΔABE) = (1/4)ar(ΔABC)

From part (i): ar(ΔABE) = (1/2)ar(ΔABD)

Since ar(ΔABD) = (1/2)ar(ΔABC):

ar(ΔABE) = (1/2) × ar(ΔABC) = ar(ΔABC)

Hence both parts are proved.

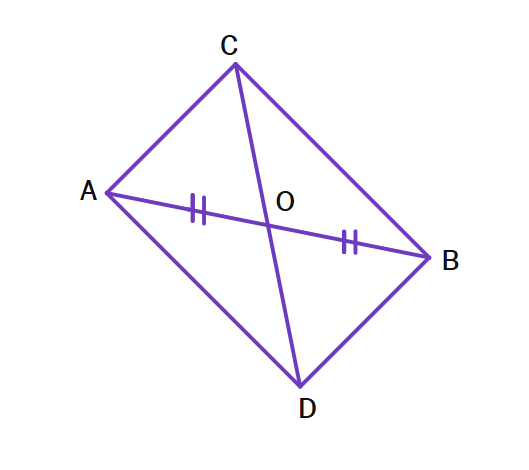
2. Show that the diagonals of a parallelogram divide it into four triangles of equal area.

Solution:

Let ABCD be a parallelogram with diagonals AC and BD intersecting at O.

In a parallelogram, diagonals each other.

So: AO = and BO =

The four triangles formed are: ΔAOB, ΔBOC, ΔCOD, ΔDOA

Comparing ΔAOB and ΔCOD:

• AO = (diagonals bisect each other)

• BO = (diagonals bisect each other)

• ∠AOB = (vertically opposite angles)

By congruence: ΔAOB ≅ ΔCOD

Therefore: ar(ΔAOB) = ar(ΔCOD)

Similarly, comparing ΔBOC and ΔDOA:

By SAS congruence: ΔBOC ≅ ΔDOA

Therefore: ar(ΔBOC) = ar(ΔDOA)

Comparing ΔAOB and ΔBOC:

Both triangles have the same base and equal heights (distance from A to OB = distance from C to OB in a parallelogram)

Therefore: ar(ΔAOB) = ar(ΔBOC)

Hence: ar(ΔAOB) = ar(ΔBOC) = ar(ΔCOD) = ar(ΔDOA) = ar(ABCD)

3. In the figure, ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that ar(ΔABC) = ar(ΔABD).

Solution:

Given: Triangles ABC and ABD on the same base , and CD is bisected by AB at O.

This means: CO =

Since both triangles have the same base AB, we need to show they have equal heights.

Let h₁ = perpendicular distance from C to AB Let h₂ = perpendicular distance from D to AB

Since O is the midpoint of CD and O lies on AB:

The perpendicular from C to AB and perpendicular from D to AB are in length.

This is because AB acts as the of CD.

Therefore: h₁ =

ar(ΔABC) = (1/2) × AB × h₁

ar(ΔABD) = (1/2) × AB × h₂

Since h₁ = h₂: ar(ΔABC) = ar(ΔABD)

Hence proved.

4. In the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that

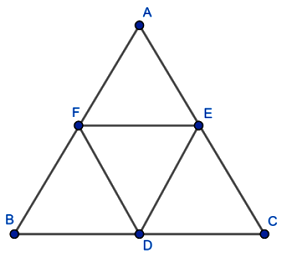
(i) BDEF is a parallelogram

(ii) ar(ΔDEF) = (1/4)ar(ΔABC)\

(iii) ar(BDEF) = (1/2)ar(ΔABC)

Solution:

Given: D, E, F are midpoints of BC, CA, AB respectively.

(i) To prove: BDEF is a parallelogram

By midpoint theorem in ΔABC:

• DE || AB and DE = AB

- Since F is midpoint of AB: BF = AB

Therefore: DE || BF and DE =

Similarly: EF || BC and EF = (1/2)BC

Since D is midpoint of BC: BD = BC

Therefore: EF || BD and EF =

Since opposite sides are parallel and equal: BDEF is a .

(ii) To prove: ar(ΔDEF) = (1/4)ar(ΔABC)

By midpoint theorem: DE = (1/2)AB, EF = (1/2)BC, DF = (1/2)AC

Triangle DEF is similar to triangle ABC with ratio .

For similar triangles, ratio of areas = (ratio of sides)²

ar(ΔDEF)/ar(ΔABC) = ()² =

Therefore: ar(ΔDEF) = ar(ΔABC)

(iii) To prove: ar(BDEF) = (1/2)ar(ΔABC)

From the midpoint theorem, the four triangles formed are: ΔAEF, ΔBDF, ΔCDE, and ΔDEF - all have areas.

Each triangle has area = ar(ΔABC)

ar(BDEF) = ar(ΔBDF) + ar(ΔDEF) = ar(ΔABC) + ar(ΔABC) = ar(ΔABC)

Hence all parts are proved.

5. In the figure D, E are points on the sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE || BC.

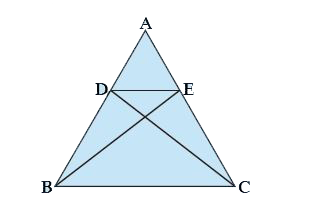
Solution:

Given: ar(ΔDBC) = ar(ΔEBC)

To prove: DE || BC

Both triangles DBC and EBC have the same base .

Since ar(ΔDBC) = ar(ΔEBC) and both have the same base: The from D and E to base BC must be equal.

This means D and E are at the same from line BC.

Since D lies on AB and E lies on AC, and both are equidistant from BC:

The line DE is to BC.

Hence: DE || BC

Hence proved.

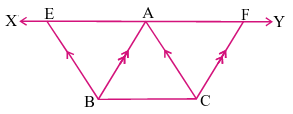
6. In the figure, XY is a line parallel to BC is drawn through A. If BE || CA and CF || BA are drawn to meet XY at E and F respectively. Show that ar(ΔABE) = ar(ΔACF).

Solution:

Given: XY || BC, BE || CA, CF || BA

To prove: ar(ΔABE) = ar(ΔACF)

Since XY || BC and BE || AC:

ABEC is a (opposite sides parallel).

Since XY || BC and CF || AB:

ABFC is a (opposite sides parallel).

Both parallelograms ABEC and ABFC have the same base .

Since XY || BC, points E and F are at the same from line AB.

Therefore: ar(parallelogram ABEC) = ar(parallelogram ABFC)

Since triangles are half the area of parallelograms with same base and height:

ar(ΔABE) = ar(ABEC)

ar(ΔACF) = ar(ABFC)

Therefore: ar(ΔABE) = ar(ΔACF)

Hence proved.

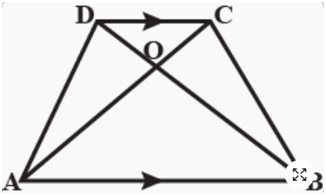
7. In the figure, diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).

Solution:

Given: ABCD is a trapezium with AB || DC, diagonals AC and BD intersect at O.

To prove: ar(ΔAOD) = ar(ΔBOC)

Consider triangles ABC and ABD:

Both have the same base and lie between the same parallel lines AB and DC.

Therefore: ar(ΔABC) = ar(ΔABD)

This can be written as:

ar(ΔABC) = ar(ΔABD)

ar(ΔAOB) + ar(ΔBOC) = ar(ΔAOB) + ar(ΔAOD)

Subtracting ar(ΔAOB) from both sides:

ar(ΔBOC) = ar(ΔAOD)

Therefore: ar(ΔAOD) = ar(ΔBOC)

Hence proved.

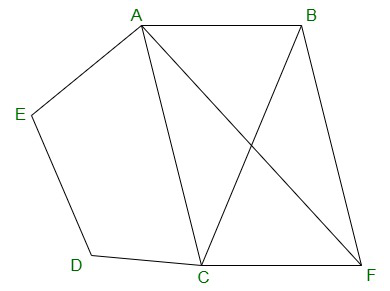
8. In the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that (i) ar(ΔACB) = ar(ΔACF) (ii) ar(ΔEDF) = ar(ΔABCDE)

Solution:

(i) To prove: ar(ΔACB) = ar(ΔACF)

Given: BF || AC

Triangles ACB and ACF have the same base .

Since BF || AC, points B and F are at the same from line AC.

Triangles with the same base and equal heights have areas.

Therefore: ar(ΔACB) = ar(ΔACF)

(ii) To prove: ar(ΔEDF) = ar(ΔABCDE)

From part (i): ar(ΔACB) = ar(ΔACF)

This means: ar(pentagon ABCDE) = ar(pentagon ABCDE) - ar(ΔACB) + ar(ΔACF)

= ar(quadrilateral ABDE) + ar(ΔACD) + ar(ΔACF) - ar(ΔACB)

= ar(quadrilateral ABDE) + ar(ΔACD) + ar(ΔACF) - ar(ΔACF)

= ar(ABDE) + ar(ΔACD) = ar()

Hence both parts are proved.

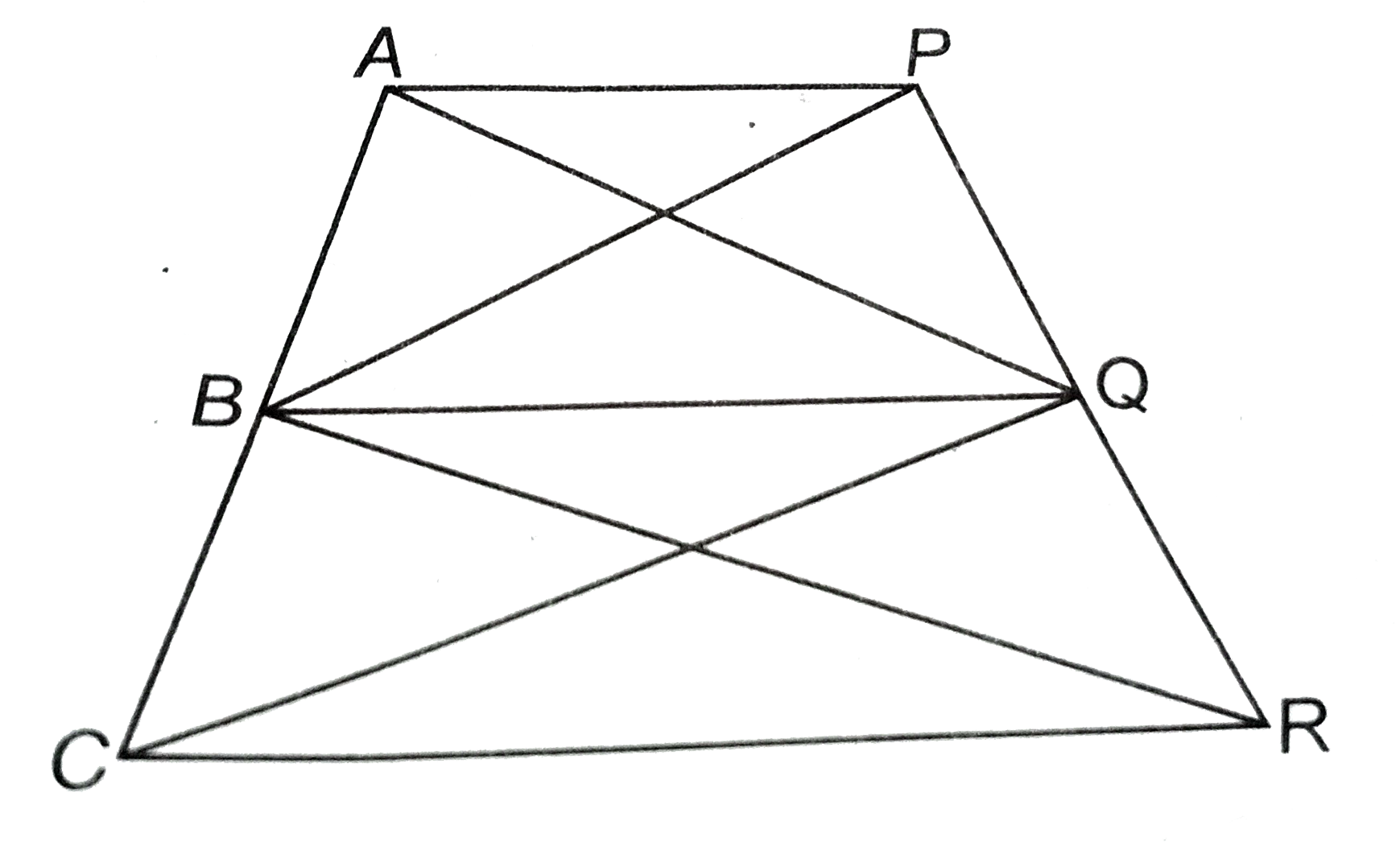
9. In the figure, if ar(ΔRAS) = ar(ΔRBS) and ar(ΔQRB) = ar(ΔPAS) then show that both the quadrilaterals PQSR and RSBA are trapeziums.

Solution:

Given: ar(ΔRAS) = ar(ΔRBS) and ar(ΔQRB) = ar(ΔPAS)

To prove PQSR is a trapezium:

From ar(ΔRAS) = ar(ΔRBS):

Both triangles have the same base .

Since areas are equal with same base, points A and B are at distance from line RS.

This means A and B lie on a line to RS.

Therefore: AB || RS, making PQSR a .

To prove RSBA is a trapezium:

From ar(ΔQRB) = ar(ΔPAS):

We can rearrange the quadrilateral areas to show that certain sides are parallel.

Since ar(ΔRAS) = ar(ΔRBS), we already established that AB || RS.

The given conditions ensure that RSBA has one pair of sides (RS and AB).

Therefore: RSBA is a .

Hence both quadrilaterals are trapeziums.

10. A villager Ramayya has a plot of land in the shape of a quadrilateral. The grampanchayat of the village decided to take over some portion of his plot from one of the corners to construct a school. Ramayya agrees to the above proposal with the condition that he should be given equal amount of land in exchange of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented. (Draw a rough sketch of plot).

Solution:

Let ABCD be Ramayya's quadrilateral plot.

Step 1: Land taken for school

Suppose the grampanchayat takes triangular portion from corner A for the school.

Step 2: Compensation land

To compensate, give Ramayya a triangular piece of land ΔABE where:

• E is chosen such that ar(ΔABE) = ar()

• E is positioned to make the final plot triangular

Step 3: Implementation

Choose point E on the extension of CD such that:

- Triangle ABE has the same as triangle ABC

- The final plot becomes triangle

Why this works:

- Land taken away = ar()

- Land given = ar()

- Net change = (equal exchange)

- Final plot shape = ADE

Construction: Draw a line through C parallel to AB, and extend it to meet the extension of AD at E. This ensures equal areas and creates a triangular final plot.