Exercise 11.2

1. The area of parallelogram ABCD is 36 cm². Calculate the height of parallelogram ABEF if AB = 4.2 cm.

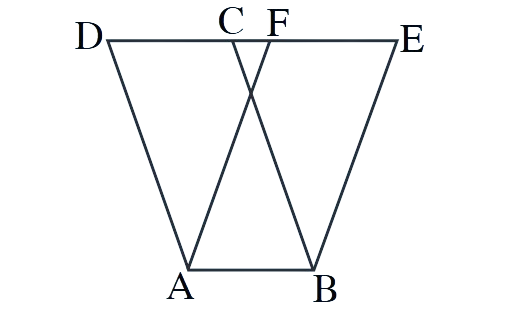
Solution:

Given: Area of parallelogram ABCD = cm² and AB = cm

We know that Area of parallelogram = base × height

For parallelogram ABCD: 36 = AB × height from C to AB

Height from C to AB = / = cm (approximately)

Since ABEF and ABCD share the same base AB and have the same height (F and C are at the same distance from AB):

Height of parallelogram ABEF = cm

2. ABCD is a parallelogram. AE is perpendicular on DC and CF is perpendicular on AD. If AB = 10 cm, AE = 8 cm and CF = 12 cm. Find AD.

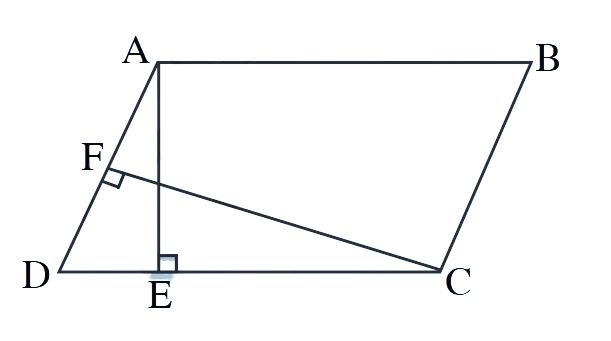
Solution:

Given: AB = cm, AE = cm, CF = cm

In a parallelogram, opposite sides are equal, so DC = = cm

Area of parallelogram ABCD using base DC and height AE:

Area = DC × AE = × = cm²

Area of parallelogram ABCD using base AD and height CF:

Area = AD × CF = AD ×

Since both expressions equal the same area:

= AD ×

AD = / = cm (approximately)

3. If E, F, G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar(EFGH) = (1/2)ar(ABCD).

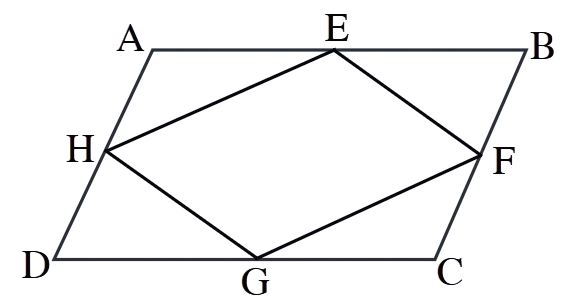
Solution:

To prove: ar(EFGH) = ar(ABCD)

Since E, F, G, H are midpoints of AB, BC, CD, AD respectively:

- AE = = AB/2

- BF = = BC/2

- CG = = CD/2

- DH = = AD/2

By the midpoint theorem, when we join midpoints of adjacent sides:

- EF is to AC and EF = AC/2

- FG is to BD and FG = BD/2

- GH is to AC and GH = AC/2

- HE is to BD and HE = BD/2

Since opposite sides are equal and parallel, EFGH is a .

The parallelogram EFGH has sides equal to the diagonals of ABCD.

By properties of midpoint quadrilaterals:

ar(EFGH) = × ar(ABCD)

Hence proved.

4. What type of quadrilateral do you get, if you join ΔAPM, ΔDPQ, ΔOCN and ΔMNB in the example 3.

Solution:

From the construction in example 3, when we join the four triangles ΔAPM, ΔDPQ, ΔOCN and ΔMNB:

The quadrilateral formed by joining these triangles is a .

This happens because:

- The triangles are formed by connecting midpoints

- The resulting figure has sides parallel and equal

- All four triangles have areas

5. P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(ΔAPB) = ar(ΔBQC).

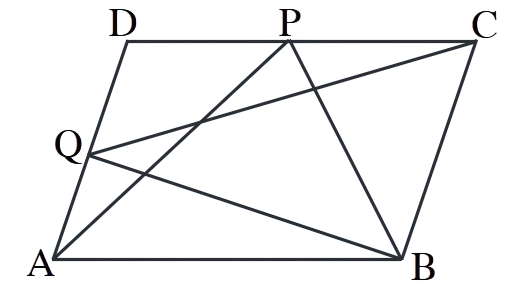
Solution:

To prove: ar(ΔAPB) = ar(ΔBQC)

Both triangles ΔAPB and ΔBQC have the same base = (opposite sides of parallelogram are equal).

Since ABCD is a parallelogram:

- P lies on DC, so distance from P to AB equals the of the parallelogram

- Q lies on AD, so distance from Q to BC equals the of the parallelogram

Both triangles have:

- Equal bases: AB =

- Equal heights: distance from P to AB = distance from Q to BC =

Therefore: ar(ΔAPB) = ar(ΔBQC) = (1/2) × base ×

Hence proved.

6. P is a point in the interior of a parallelogram ABCD. Show that

(i) ar(ΔAPB) + ar(ΔPCD) = (1/2)ar(ABCD)

(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD)

(Hint: Through P, draw a line parallel to AB)

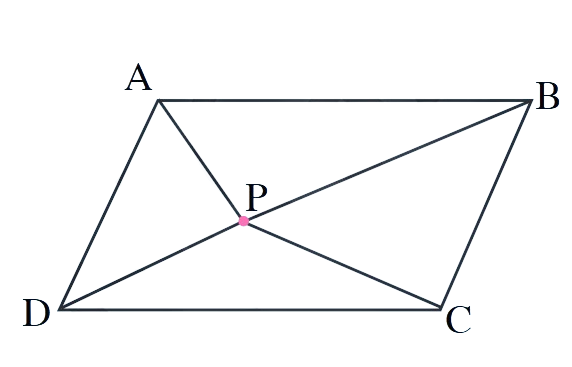
Solution:

Draw a line through P parallel to AB, meeting AD at M and BC at N.

(i) To prove: ar(ΔAPB) + ar(ΔPCD) = (1/2)ar(ABCD)

Since MN is parallel to AB:

• ABMN is a

- MNCD is a

ar(ΔAPB) = ar(ΔAMP) + ar(ΔPMB)

Since ABMN is a parallelogram: ar(ΔAPB) = ar(ABMN)

ar(ΔPCD) = ar(ΔPMC) + ar(ΔPCN)

Since MNCD is a parallelogram: ar(ΔPCD) = ar(MNCD)

ar(ΔAPB) + ar(ΔPCD) = (1/2)ar(ABMN) + (1/2)ar(MNCD) = [ar(ABMN) + ar(MNCD)] = ar(ABCD)

(ii) To prove: ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD)

From part (i): ar(ΔAPB) + ar(ΔPCD) = ar(ABCD)

Similarly, ar(ΔAPD) + ar(ΔPBC) = ar(ABCD)

Therefore: ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD)

Hence both parts are proved.

7. Prove that the area of a trapezium is half the sum of the parallel sides multiplied by the distance between them.

Solution:

Let ABCD be a trapezium with AB || CD, where AB and CD are the parallel sides.

Let h be the between the parallel sides AB and CD.

Draw diagonal AC to divide the trapezium into two triangles: ΔABC and ΔACD.

Area of ΔABC = (1/2) × AB ×

Area of ΔACD = (1/2) × CD ×

Area of trapezium ABCD = Area of ΔABC + Area of ΔACD

= (1/2) × AB × h + (1/2) × CD × h

= (1/2) × h × ( + )

= (1/2) × (sum of parallel sides) ×

Hence proved.

8. PQRS and ABRS are parallelograms and X is any point on the side BR. Show that (i) ar(PQRS) = ar(ABRS) (ii) ar(ΔAXS) = (1/2)ar(PQRS)

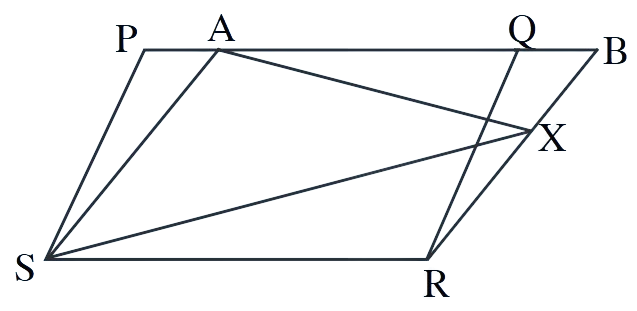
Solution:

(i) To prove: ar(PQRS) = ar(ABRS)

Both parallelograms PQRS and ABRS have the same base .

Since PQ || RS and AB || RS, points P, Q and A, B lie on lines to RS.

Both parallelograms have the same (distance between the parallel lines).

Therefore: ar(PQRS) = ar(ABRS) = base ×

(ii) To prove: ar(ΔAXS) = (1/2)ar(PQRS)

ΔAXS and parallelogram PQRS have the same base (or consider RS as common).

Since X lies on BR and AB || RS, the height of ΔAXS from vertex X to base AS equals the of parallelogram PQRS.

Area of triangle = (1/2) × base × height

Area of parallelogram = base × height

Therefore: ar(ΔAXS) = × ar(PQRS)

Hence both parts are proved.

9. A farmer has a field in the form of a parallelogram PQRS as shown in the figure. He took the mid-point A on RS and joined it to points P and Q. In how many parts is the field divided? What are the shapes of these parts? The farmer plans to sow groundnuts in an area equal to the combined area of pulses and paddy. How should he proceed to sow the seeds and why?

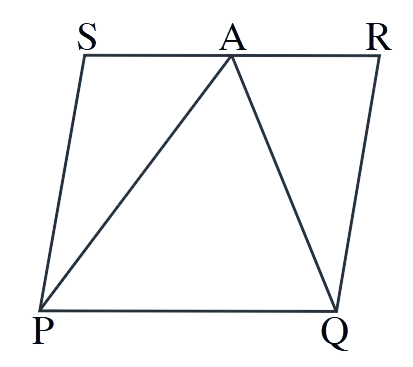
Solution:

When point A (midpoint of RS) is joined to P and Q:

Number of parts: The field is divided into parts.

Shapes: The three parts are:

1. Triangle

2. Triangle

3. Triangle

Areas: Since A is the midpoint of RS:

- ar(ΔPAS) = ar(ΔPAQ) (same base PA, equal heights from S and Q)

- ar(ΔQAS) = × ar(ΔQRS)

For groundnuts area = pulses area + paddy area:

If pulses are grown in ΔPAS and paddy in ΔQAS, then:

Groundnuts area = ar(ΔPAS) + ar(ΔQAS) = ar()

Reason: Since A is the midpoint, triangle PAQ has area equal to the combined area of triangles PAS and QAS.

Therefore, he should sow in triangle PAQ, in triangle PAS, and in triangle QAS.

10. Prove that the area of a rhombus is equal to half of the product of the diagonals.

Solution:

Let ABCD be a rhombus with diagonals AC and BD intersecting at O.

In a rhombus, the diagonals are to each other and each other.

Let AC = d₁ and BD = d₂ be the lengths of the diagonals.

Since diagonals bisect each other:

- AO = OC =

- BO = OD =

The rhombus is divided into 4 right triangles: ΔAOB, ΔBOC, ΔCOD, ΔDOA.

Area of each triangle:

- ar(ΔAOB) = (1/2) × AO × BO = (1/2) × (d₁/2) × (d₂/2) = d₁d₂/8d₁d₂/4

- All four triangles have areas

Total area of rhombus = 4 × (d₁d₂/8) =

Therefore: Area of rhombus = (1/2) × × = (1/2) × (product of diagonals)

Hence proved.