Diagonals of a Parallelogram
Now, let's look at some properties of the diagonals of a parallelogram.
Theorem : The diagonals of a parallelogram bisect each other.
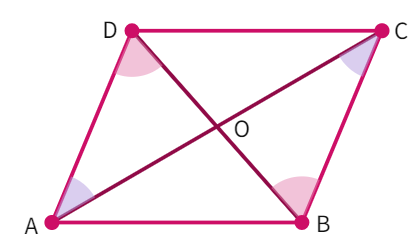
- We have parallelogram ABCD with AB || DC and AD||BC.
- Considering triangles ∆ AOD and ∆ COB, we get: AD =
as sides are equal - ∠ DAO = ∠
and ∠ ADO = ∠ ( interior angles are equal) - By
congruency, ∆ AOD ≅ ∆ - By CPCT, AO =
and BO = - Thus, diagonals of a parallelogram bisect each other.
Theorem: If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
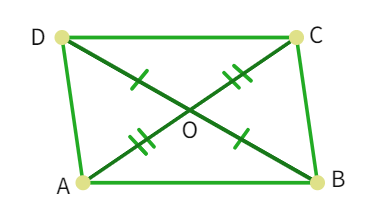
- We have been given: OA = OC and OB = OD
- Considering the triangles ∆ AOB and ∆ COD: ∠ AOB = ∠
(vertically angles) - OA =
and = OD - ∆
≅ ∆ COD by congruency rule. - Therefore, ∠ OAB = ∠
- These are alternate interior angles to the lines AB and CD and are
. - Thus, AB ||
- A similar argument can made for ∆ AOD and ∆ COB, which gives us: BC ||
- Since, quadrilateral ABCD has parallel opposite sides, ABCD is a
.
Example 2: Prove that the diagonals of a rhombus are perpendicular to each other.
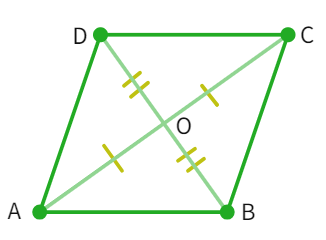
- Rhombus is a
having . - Thus, from the figure: AB =
= CD = - Considering, the triangles ∆ AOD and ∆ COD, we get: OA = OC ( as
) - OD =
as it is a side - AD =
(given) - By
congruency rule: ∆ AOD ≅ ∆ - By CPCT, we get: ∠ AOD = ∠
- We also know that: ∠ AOD + ∠ COD =
° - Thus, we get:
∠ AOD = 180° which further gives us: ∠ AOD = ° - Thus, the diagonals of a rhombus are perpendicular to each other.
Example 3: ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || AB. Show that:
(i) ∠ DAC = ∠ BCA
(ii) ABCD is a parallelogram
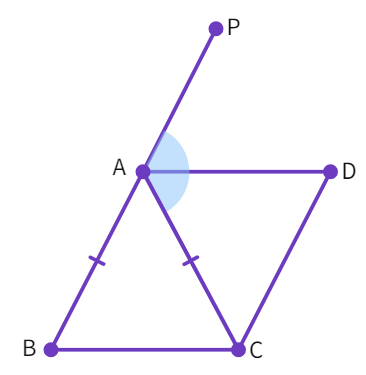
- Given: ∆ ABC is isosceles in which AB = AC
- Thus, ∠ ABC = ∠
(Angles to equal sides) - Using exterior angle property: ∠ PAC = ∠ ABC + ∠
- Which gives us: ∠ PAC =
∠ ACB (i) - Also given: AD bisects ∠ PAC i.e. ∠ PAC = 2 ∠
(ii) - Combining (i) and (ii) we get: ∠ DAC = ∠
- Further on, equal angles ∠ DAC and ∠ ACB form a pair of alternate angles where line segments BC and AD are intersected by a transversal line
. - Thus, BC ||
- Also given: BA ||
- Since the opposite sides of the quadrilateral ABCD are parallel, ABCD is a
.
Example 4: Two parallel lines l and m are intersected by a transversal p. Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
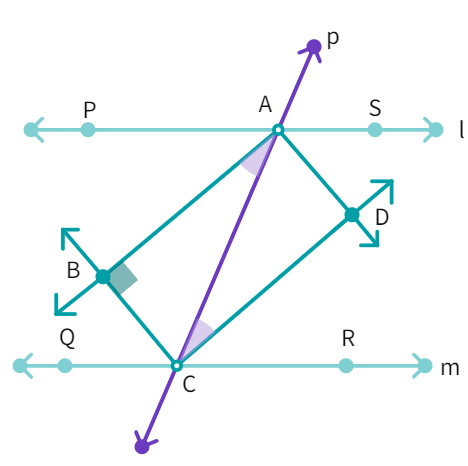
- Given: PS || QR and transversal p intersects them at points A and C respectively.
- Also given: The bisectors of ∠ PAC and ∠ ACQ intersect at B and bisectors of ∠ ACR and ∠ SAC intersect at D.
- From the figure: ∠ PAC = ∠ ACR (Alternate angles as l || m and p is a transversal)
- Thus,
1 2 ∠ ACR which gives us ∠ = ∠ - Equal angles ∠ BAC and ∠ ACD form a pair of alternate angles for the lines AB and DC with
as transversal. - So, AB ||
- Similarly, we can conclude that angles ∠ ACB = ∠
- Thus, BC ||
- Therefore, quadrilateral ABCD is a
- From the figure: ∠ PAC + ∠ CAS =
° - Dividing the whole equation by
1 2 + ∠ = ° - This gives us ∠ BAD =
° - Since, ABCD is a parallelogram with one angle equal to 90°, it is a rectangle.
Example 5 : Show that the bisectors of angles of a parallelogram form a rectangle.
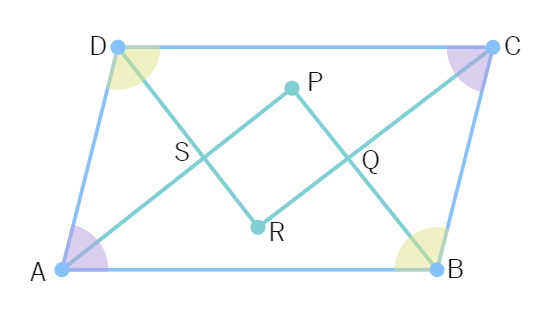
Solution:
